| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 교육
- 적분
- Maths
- integral
- division
- equation
- t-치환
- fractions
- differential
- Weierstrass
- GCSE
- solution
- College
- 치환
- Admissions
- algebraic
- DENOMINATOR
- Order
- Partial
- factor
- triangle
- factors
- 학년
- test
- 바이어슈트라스
- Oxford
- mathematics
- 제도
- 영국
- a-level
- Today
- Total
목록분류 전체보기 (81)
Cambridge Maths Academy
We have: 11=101=010=100=1 Are you surprised by 00=1? Proof. To prove this, we consider y=xx and take the limit x→0. It is not straightforward to do this directly with xx so we take the (natural or any) logarithm on both sides: lny=lnxx=xlnx Let $x=e^{-n}..
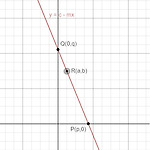 10. A challenging geometry question (STEP level)
10. A challenging geometry question (STEP level)
수학 모음 (Maths collection) 전체보기 Question. The line L has equation y=c−mx, with m>0 and c>0. It passes through the point R(a,b) and cuts the axes at the points P(p,0) and Q(0,q), where a,b,p and q are all positive. Find p and q in terms of a,b and m. As L varies with R remaining fixed, show that the minimum value of the sum of the distances of P and $Q..
In mathematics, we encounter terms, equations, expressions, inequalities and identities. 7xy is a term. 5x−2=8 is an equation. 7x2+3x is an expression. $5x-2
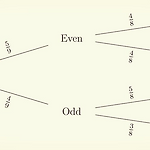 9. Three cards with an even score (GCSE)
9. Three cards with an even score (GCSE)
수학 모음 (Maths collection) 전체보기 Question. Rebecca has 9 cards, each with a number on them. The numbers are: 2,2,3,4,5,6,6,7,9 She picks three cards at random without replacement. Rebecca multiplies three numbers to get a score. Calculate the probability that the score is an even number. Solution. Let's consider: the ca..
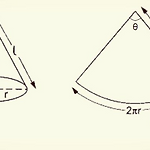 19. 원뿔의 표면적 구하기
19. 원뿔의 표면적 구하기
원뿔의 표면적을 구하기 위해서 전개도를 고려한다. 전개도는 원뿔을 잘라 펼친 그림의 의미한다. 전개도에서 부채꼴(sector)의 넓이와 원의 넓이를 구한 다음 둘의 넓이를 더하면 된다. 부채꼴의 넓이: 부채꼴 안에 있는 각도 θ를 구해야 하는데, 이는 호의 길이를 고려하여 구할 수 있다. L=2πℓ×θ360=2πr⇒ℓ×θ360=r 부채꼴(sector)의 넓이: $$ \begin{align} A_{\rm sector}&=\pi\ell^2\times\frac{\theta}{360} \\ &=\pi\ell\times..
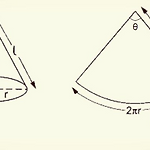 19. Surface area of a circular cone
19. Surface area of a circular cone
수학 모음 (Maths collection) 전체보기 To find the surface area of a circular cone, we need to consider the area of the circular sector and the area of the circle. The area of the circular sector: We find the angle θ by considering the arc length, i.e. L=2πℓ×θ360=2πr⇒ℓ×θ360=r The area is then $$ ..
Pure mathematics Year 1 Table of contents Introduction Factorial n! and arrangements Permutations (nPr) Combination: n choose r An alternative derivation of the formula for 'n choose r' 0! = 1 revisited Pascal's triangle using combinations Examples Edexcel P1 Ch8 Exercise 8B 1. Introduction While Pascal's triangle is a convenient tool, for large values of the index, n, it takes a long ..
Pure mathematics Year 1 Table of contents Binomial, trinomial and polynomial Binomial expansion Pascal's triangle Examples Edexcel P1 Ch8 Exercise 8A 1. Binomial, trinomial and polynomial The binomial expansion tells us how to expand (a+b)n. The word 'bi-nomial' means 'two terms' - here, they are a and b. Similarly, monomial means 'one term', trinomial means 'three terms' and polynomial m..
