| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- solution
- Weierstrass
- test
- algebraic
- Order
- Oxford
- 학년
- 교육
- division
- 제도
- differential
- 적분
- mathematics
- College
- a-level
- GCSE
- Partial
- equation
- fractions
- integral
- triangle
- factors
- t-치환
- DENOMINATOR
- 바이어슈트라스
- Maths
- 치환
- Admissions
- 영국
- factor
- Today
- Total
Cambridge Maths Academy
9. Three cards with an even score (GCSE) 본문
9. Three cards with an even score (GCSE)
Cambridge Maths Academy 2021. 1. 14. 10:03수학 모음 (Maths collection) 전체보기
Question. Rebecca has 9 cards, each with a number on them. The numbers are: 2,2,3,4,5,6,6,7,9
She picks three cards at random without replacement. Rebecca multiplies three numbers to get a score.
Calculate the probability that the score is an even number.
Solution. Let's consider:
- the case where Rebecca picks one card,
- the case where she picks two cards,
- and the case where she picks three cards
in order to establish our answer to the question.
1) One card
If Rebecca picks one card, it is either even or odd (i.e. there are 2 possibilities) and we find the following probabilities: P(even)=59P(odd)=49
2) Two cards
If Rebacca picks two cards and multiplies them to get a score, there are a total of 9×8=72 possibilities. If we only consider whether each individual card is even or odd, we have the following 4 cases:
| (1st card, 2nd card) | #Possibilities |
| (even, even) | 5×4=20 |
| (even, odd) | 5×4=20 |
| (odd, even) | 4×5=20 |
| (odd, odd) | 4×3=12 |
To get an even score, we should have: even×eveneven×oddodd×even
thus we find P(evenscore)=P(even,even)+P(even,odd)+P(odd,even)=20+20+2072=6072=56
Alternative: We could alternatively exclude the (odd×odd) case from the possibilities, i.e. P(evenscore)=1−P(odd,odd)=1−1272=1−16=56✓
Aside. Tree diagram: We can represent this using a tree diagram.

where P(even,even)=59×48=2072=518P(even,odd)=59×48=2072=518P(odd,even)=49×58=2072=518P(odd,odd)=49×38=1272=16
3) Three cards
For three cards, there are a total of 9×8×7=504 possibilities. If we only consider whether each individual card is even or odd, we have the following 8 cases:
| (1st card, 2nd card, 3rd card) | #Possibilities |
| (even, even, even) | 5×4×3=60 |
| (even, even, odd) | 5×4×4=80 |
| (even, odd, even) | 5×4×4=80 |
| (even, odd, odd) | 5×4×3=60 |
| (odd, even, even) | 4×5×4=80 |
| (odd, even, odd) | 4×5×3=60 |
| (odd, odd, even) | 4×3×5=60 |
| (odd, odd, odd) | 4×3×2=24 |
To get an even score, we should have: even×even×eveneven×even×oddeven×odd×eveneven×odd×oddodd×even×evenodd×even×oddodd×odd×even
or, it would be easier to exclude the (odd×odd×odd) case from the possibilities, i.e. P(evenscore)=1−P(odd,odd,odd)=1−24504=1−121=2021
Aside. Tree diagram: We can represent this using a tree diagram.
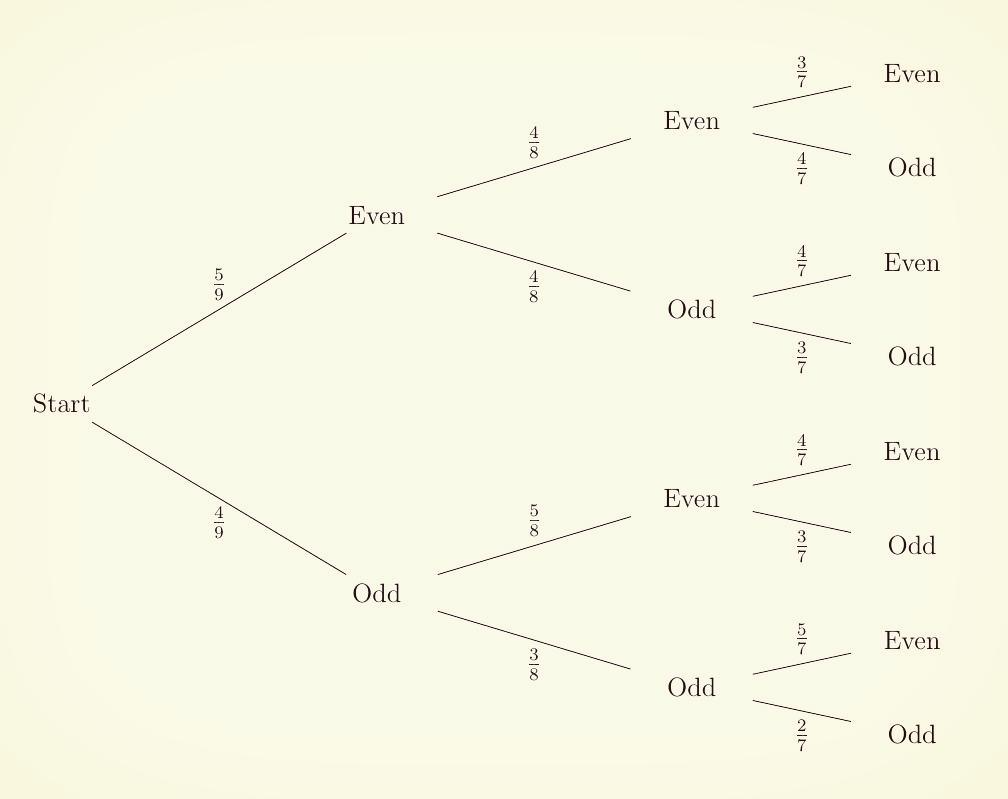
where P(even,even,even)=59×48×37=60504=542P(even,even,odd)=59×48×47=80504=1063P(even,odd,even)=59×48×47=80504=1063P(even,odd,odd)=59×48×37=60504=542P(odd,even,even)=49×58×47=80504=1063P(odd,even,odd)=49×58×37=60504=542P(odd,odd,even)=49×38×57=60504=1063P(odd,odd,odd)=49×38×27=24504=121
A student's question: Suppose that we have six cards. 1,2,3,4,5,6 When we pick two cards and work out the probability to get, say, a three and a four, we consider both the cases, (3,4) and (4,3). On the other hand, when working out the probability to get two lots of three's, we count (3,3) only once. Why is this? Do we not need to count (3,3) twice?
Answer. This is
- partly due to (in)distinguishability of the pair, i.e. (3,4) and (4,3) are distinguishable whereas (3,3) and (3,3) are not,
- and partly to do with what the question wants.
Step 1. Let's consider the following four questions:
- What is the probability for (1st card, 2nd card) = (3,3)? P(3,3)=P(3)×P(3)
- What is the probability for (1st card, 2nd card) = (3,4)? P(3,4)=P(3)×P(4)
- What is the probability for (1st card, 2nd card) = (4,3)? P(4,3)=P(4)×P(3)
- What is the probability for (1st card, 2nd card) = (4,4)? P(4,4)=P(4)×P(4)
They are all worked out the same way and each time we consider the relevant case only. In other words, if we specify what we should get for the 1st and 2nd cards, there is no difference whether we pick the same number twice or two different numbers.
Step 2. Now, consider the following two questions:
- What is the probability to get a three and a three?
- What is the probability to get a three and a four?
Due to indistinguishability, 'What is the probability to get a three and a three?' is the same question as 'What is the probability for (1st card, 2nd card) = (3,3)?'. In other words, for indistinguishable cases such as (3,3), whether we specify the 1st and 2nd cards or not makes no difference. P(a three and a three)=P(3,3)
However, 'What is the probability to get a three and a four?' contains two questions as 'a three and a four' can arise in two different ways, namely, (3,4) and (4,3), In other words, for distinguishable cases, whether we specify the 1st and 2nd cards does make a difference. P(a three and a four)=P((3,4)or(4,3))=P(3,4)+P(4,3)
In summary, 'What is the probability to get a three and a three?' and 'What is the probability to get a three and a four?' appear to be the same kind of question but they are different. We can see the difference by comparing them to where we specify the order of the cards, i.e.
- What is the probability to get a three and a three? = What is the probability for (1st card, 2nd card) = (3,3)?
- What is the probability to get a three and a four? ≠ What is the probability for (1st card, 2nd card) = (3,4)?
'수학 모음 (Maths collection) > Technical B - Problem solving' 카테고리의 다른 글
| 11. A problem on coordinate geometry (GCSE) (0) | 2021.02.27 |
|---|---|
| 10. A challenging geometry question (STEP level) (0) | 2021.01.26 |
| 8. Some integrals (0) | 2020.12.31 |
| 7. Differentiation - Some inverse trigonometric functions (0) | 2020.12.31 |
| 6. Probability - Jumping goldfish (GCSE) (0) | 2020.12.29 |