| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 바이어슈트라스
- integral
- 치환
- 영국
- differential
- equation
- factor
- Maths
- triangle
- solution
- DENOMINATOR
- GCSE
- College
- 교육
- Oxford
- Order
- fractions
- 적분
- Weierstrass
- 제도
- Partial
- factors
- t-치환
- division
- 학년
- a-level
- test
- algebraic
- Admissions
- mathematics
- Today
- Total
Cambridge Maths Academy
[A-level 수학 수업] Cambridge Maths Academy 본문
케임브리지 대학교 수학 전공 선생님과 A-level Maths, Further maths 온라인 수업(1:1/그룹) 진행 중입니다.
자세한 수업 내용과 선생님 이력은 아래 사진을 참조해 주시기 바랍니다.

★ 선생님 약력: (사진 참조)
- 케임브리지 대학교 수학과 학부, 석사 졸업. 박사과정 수료 (전액장학금 수여)
- 10년 이상 A-level 수학 지도
- A-level Maths A* (594/600), Further maths A* (597/600), Physics A* (596/600), Chemistry A* (565/600)
- STEP I, II, III Outstanding(S)
- British Maths Olympiad: Gold medal (Top 50 in the nation Award)
- 3년간 STEP Exams 채점자 (OCR)
★ 수업료: Maths £70/hour, Further maths £80/hour. (1회 수업 시간은 90분 = 1.5시간입니다.)
★ 문의: 07491 906433, cma.edu7@gmail.com
수업 중 전화를 받지 못하는 경우에는 문자를 남겨주시기 바랍니다.
첫 수업에 앞서 전반적인 이해도를 파악하기 위해 소량의 문제 풀이 과제가 주어집니다.
대부분의 학생들이 13학년 마지막 시험이 끝날 때까지 수업을 이어갈 만큼 저희는 선생님의 실력을 자부합니다만, 우선 첫 수업을 경험해 보시고 추가 진행 여부를 결정하시면 좋겠습니다.
★ 수업 방향: 뭐니뭐니해도 수학 공부의 핵심은 '원리 이해'와 이를 확인하고 숙지하는 '문제 풀이'입니다.
지금까지 수학 공부를 하면서 '수학은 암기가 아니라고 했는데, 막상 공식을 외워서 적용하는 게 많다. 공식을 쓰면 답이 나오긴 하는데, 도대체 어떤 원리로 그렇게 되는 것인지 궁금하다' 등의 답답함을 느낀 학생들이 저희 수업에서 큰 효과를 봅니다.
공식을 단순히 외우는 데서 그치지 않으려면, 기본 원리에서부터 공식을 유도하는 과정에 익숙해져야 합니다. 공식의 유도 과정을 알지 못하면 그 공식을 언제, 어떻게 써야하는지에 대한 완전한 이해가 생기기 어렵기 때문입니다. 또한, 이해가 부족한 상태에서는 문제를 풀고도 내 실력으로 해냈다는 확신이 생기지 않고, 실력이 차곡차곡 쌓여가는 자신감을 갖기가 어렵습니다. 결국 어려운 응용 문제가 나오면 겁부터 나게 되죠. 문제를 많이 푸는 것도 중요하지만, 원리를 이해한 상태에서 연습을 해야 '내 것'이 되고 경험치가 쌓이게 됩니다. 독에 구멍이 있으면 그것부터 막아야지, 구멍은 그대로 둔 채 바가지를 바꿔가며 물 담는 경험치를 늘인다고 해서 독이 채워지지 않는 것과 같습니다.
흔히 수학은 암기과목이 아니라고 합니다. 분명 맞는 말입니다. 그런데도 막상 공부를 해보면 일정 정도의 기억력을 요구합니다. 즉, 이유를 모른 채 외우는 '암기'가 아니라, 이해를 바탕으로 원리와 결과물을 떠올리는 '기억'이 요구되는 것이죠. 과정에 대한 이해가 수반되어야 암기가 아닌 기억으로 넘어갈 수 있습니다. 그리고 이때는 과정을 '기억하기' 보다는 저절로 '기억되는' 것에 가깝습니다. 가령, 동네 마트에서 집까지 가는 길을 종이에 적어가며 '암기'하는 사람은 없을 겁니다. 처음엔 어색했던 그 길을 반복해서 다니다 보면 어느새 자연스레 기억을 하게 되는 것이지요. 수학 공부도 마찬가지가 아닐까 생각합니다. 원리부터 공식까지 이르는 길을 반복해서 다니다 보면 그 과정과 결과가 자연스레 기억됩니다.
★ 수업 진행방식: 줌(zoom)과 함께 아이패드 Notability 앱으로 수업을 진행합니다. 아래 사진을 통해 수업 수업 노트의 일부를 확인하실 수 있습니다. 매수업 후 수업 노트는 학생에게 pdf 파일로 전송됩니다.
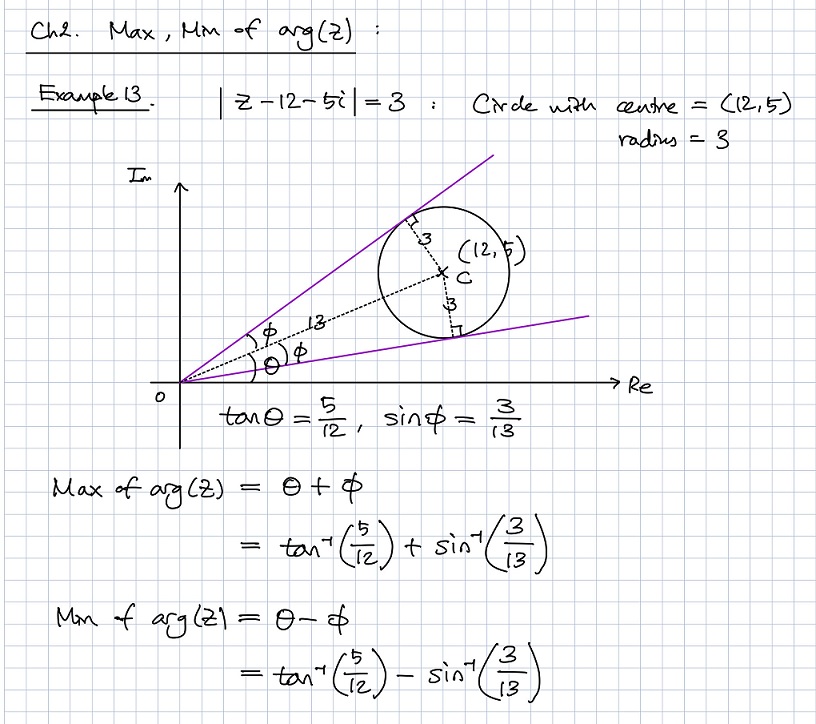
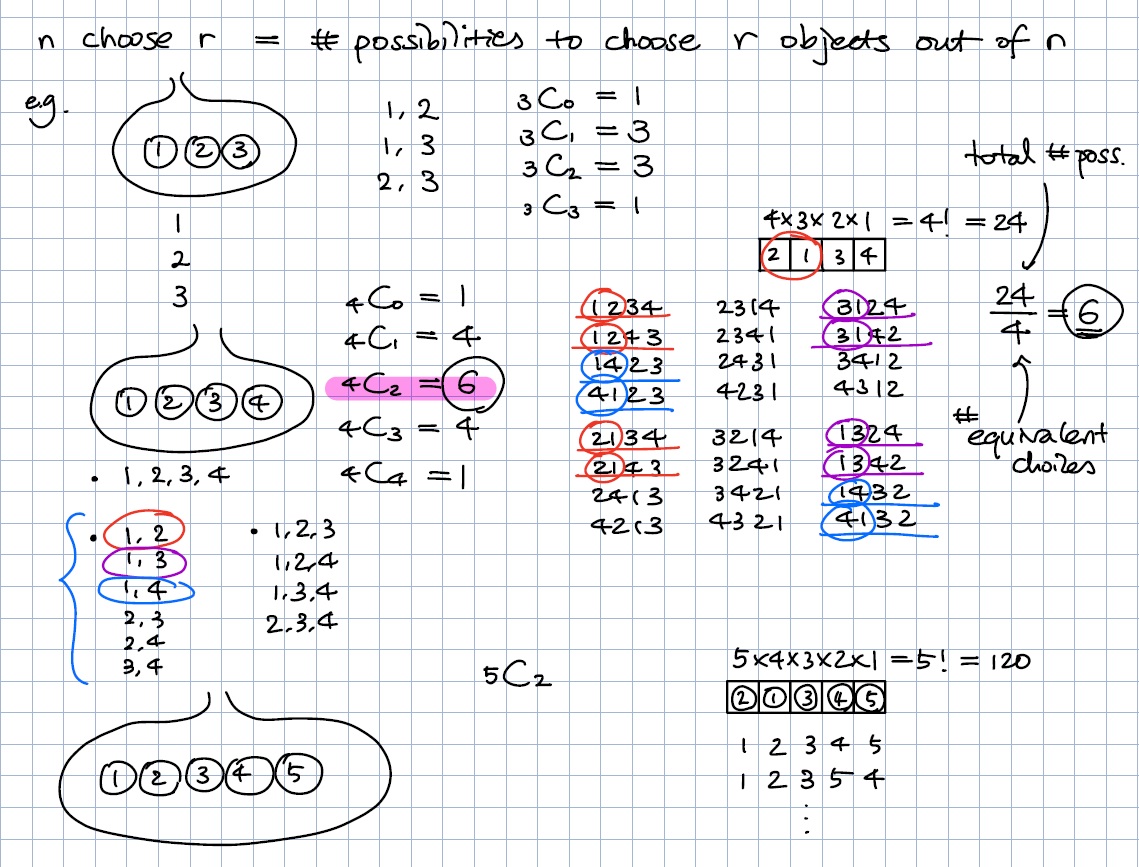
★ 숙제: 앞서 원리를 이해하고 난 뒤 그걸 반복해서 익히는 과정의 중요성을 강조했지요. 수업 시간에 이루어진 이해를 바탕으로 배운 내용을 내 것으로 만드는 과정이 수업 못지 않게 중요합니다. 그리고 이 부분이 '원리 이해 + 문제 풀이' 중 문제 풀이에 해당됩니다.
특히 A-level 수학부터는 한 번 설명을 들으면 머릿 속에 각인되는 '직관적인 내용'보다는, 정의를 익히고 난 뒤 다양한 연습을 통해 '숙지'해야 하는 내용이 늘어나기 때문에, 수업이 끝난 후 복습은 필수입니다. 공부하다가 '아, 저 내용을 들어는 봤는데, 배운 적은 있는데 자세히는 기억이 안 난다'고 느낀다면, 내 것으로 만드는 숙지 과정이 충분하지 않았음을 뜻합니다.
복습은 수업을 마치고 가능하면 가까운 시간 내에 하는 것이 효과가 좋습니다. 또, 한 번만 하는 것이 아니라 주기적으로 반복하여 배운 내용을 '내 것'으로 만들어 가야 합니다. 저희는 이를 날짜별 숙제를 통해 해나가고 있습니다.
숙제를 내어주면 대개 미뤘다가 다음 수업 전날 몰아서 하는 경우가 많은데, 복습 효과를 최대로 누리기 위해 매수업 후 날짜별로 숙제가 주어집니다. 날짜별 숙제를 경험한 학생들의 피드백을 보면 대부분 '한 번 밀리면 따라잡기 어렵기 때문에 수학 숙제 만큼은 밀리지 않도록 노력했다'는 말들을 많이 합니다. 그리고 수학 공부에서 배운 요령을 다른 과목에도 적용시키는 기지를 발휘하는 학생들은 다른 과목에서도 그 효과를 보곤 하지요. 아래는 날짜별 숙제의 실제 예시입니다.
==
Day 1
Ch12 Examples 17,18
Exercise 12I (p.276) Q3,4
Day 2
Ch12 Example 16,
Exercise 12I (p.276) Q5 (여기서는 stationary point 양쪽의 점들을 고려하여 local max/min/point of inflection을 정하라고 함. 이 방법에 대한 도움이 필요하면 다음 시간에 질문할 것.)
Exercise 12I (p.276) Q6,7 Exercise 12B Q2,3,4,5,6,7
Day 3
Exercise 8E Q3,4,7,8,9 Exercise 1A Q3(c)(f)(i)(l)(o)(r)
Exercise 12C Q1,2,3,4
Day 4
Exercise 1F Q1(d)(h),Q2(c)(h)(m),Q3(c)(f), Q4
Mixed exercise 8 Q9,10,11,12
Day 5
Mixed exercise 1 Q15,16,17,18,19,20,21,22,23,24,Challenge (문제는 많지만 오래 걸리지 않음)
Mixed exercise 8 Q13,14,15,16
==
★ 대학 입시의 큰 관문 Interview
케임브리지, 옥스포드 입학에서 면접(interview)은 필수 과정으로, 가장 어려운 관문이기도 합니다. 임페리얼 컬리지에서도 면접을 보는 대상과 폭을 점차 늘리고 있습니다.
대입 인터뷰에서는 다소 수준 높은 문제를 중심으로 원리를 제대로 이해하는 지를 점검하려고 합니다. 과목의 본질을 깊이 이해하는 학생과 시험 점수만 높은 학생을 구분하기 위함이지요. CMA 수업에서는 원리 중심의 수업을 통해 평소 인터뷰 훈련이 자연스럽게 이루어지도록 합니다.
