| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- integral
- 영국
- fractions
- division
- 교육
- 적분
- a-level
- equation
- 제도
- triangle
- Oxford
- 치환
- DENOMINATOR
- factor
- Maths
- Weierstrass
- Order
- test
- differential
- 바이어슈트라스
- t-치환
- solution
- Admissions
- Partial
- mathematics
- GCSE
- factors
- 학년
- algebraic
- College
- Today
- Total
목록적분 (6)
Cambridge Maths Academy
수학 모음 (Maths collection) 전체보기 Question. Let $$ \begin{align} I_n = \int \sin^n(ax) \, \textrm{d}x \end{align} $$ (a) Show that $$ \begin{align} I_n = -\frac1{an} \sin^{n-1}(ax) \cos(ax) + \frac{n-1}{n}I_{n-2} \end{align} $$ Let $$ \begin{align} J_n = \int_0^{\frac{\pi}{2}} \sin^nx \, \textrm{d}x \end{align} $$ (b) Hence, or otherwise, show that $$ \begin{align} J_n = \frac{n-1}{n}J_{n-2} \end{al..
Question. 다음 적분을 구하라. $$ \begin{align} {\rm (a)}&& &\int\frac{1}{\sqrt{1-3x^2}}\,dx \\ {\rm (b)}&& &\int\frac{x}{4x^2+8x+13}\,dx \\ {\rm (c)}&& &\int_0^1\arcsin x\,dx \end{align} $$ Solution. (a) 치환적분(Integration by substitution)을 사용하여 $$ \begin{align} x&=\frac1{\sqrt{3}}\sin u \\ \Rightarrow\quad dx&=\frac1{\sqrt{3}}\cos u\,du \\ \end{align}$$ 다음과 같이 적분할 수 있다. $$ \begin{align} I_1 &=\int\frac{1..
수학 모음 (Maths collection) 전체보기 1. $u={\rm csch}\,x+\coth x$ 치환적분 $$ \int{\rm csch}\,x\,\textrm{d}x=-\ln\vert{\rm csch}\,x+\coth x\vert+c $$ 첫 번째 시도로 코시컨트의 적분에서처럼 자연로그를 시도할 수 있다. 쌍곡시컨트(sech)와 달리 쌍곡코시컨트는 삼각함수와 쌍곡선함수의 도함수에 마이너스 차이가 없기 때문에 자연로그 적분이 가능하다는 것을 알게 된다. 우리에게 필요한 도함수들은 다음과 같다. $$ \begin{align} \frac{\textrm{d}}{\textrm{d}x}\csc x&=-\csc x\cot x & \frac{\textrm{d}}{\textrm{d}x}{\rm csch}\,x&..
수학 모음 (Maths collection) 전체보기 0. $\int{\rm sech}\,x\,\textrm{d}x=\ln\vert{\rm sech}\,x+\tanh x\vert+c\,$? 첫 번째 시도로 시컨트의 적분에서처럼 자연로그를 시도할 수 있다. 그러나 삼각함수와 쌍곡선함수의 도함수에서 마이너스 차이로 인해 가능하지 않다는 것을 알게 된다. 이 차이점을 아는 것도 중요하므로 이 부분부터 살펴보자. 우리에게 필요한 도함수들은 다음과 같다. $$ \begin{align} \frac{\textrm{d}}{\textrm{d}x}\tan x&=\sec^2x & \frac{\textrm{d}}{\textrm{d}x}\tanh x&={\rm sech}^2x \\ \frac{\textrm{d}}{\textrm..
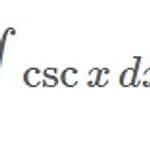 3. 코시컨트/코세칸트(cosec x, csc x)의 적분법 | Integration of cosec x
3. 코시컨트/코세칸트(cosec x, csc x)의 적분법 | Integration of cosec x
코시컨트의 적분은 시컨트와 매우 유사하다. (시컨트 적분의 역사적 배경은 이곳 참조.) 이 글에서는 코시컨트/코세칸트의 적분을 4가지 방법으로 유도해보자. $$ \begin{align} \int \csc x \, \textrm{d}x &= - \ln \vert \csc x + \cot x \vert + c \\ &= \frac12 \ln \left\vert \frac{1-\cos x}{1+\cos x}\right\vert + c \\ &= \ln \left\vert \tan \frac{\pi}{2}\right\vert + c \end{align} $$ 1. $u=\csc x+\cot x$ 치환적분 $$ \int\csc x\,\textrm{d}x=-\ln\vert\csc x+\cot x\vert+c $$ ..
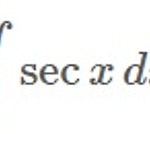 2. 시컨트/세칸트(sec x)의 적분법 | Integration of sec x
2. 시컨트/세칸트(sec x)의 적분법 | Integration of sec x
수학 모음 (Maths collection) 전체보기 0. 역사적 배경 시컨트/세칸트 함수 적분의 역사는 16세기 말~17세기 초, 항해(sea navigation)와 그에 필요한 지도 제작 시기로 거슬러 올라간다. 1569년 벨기에 지도학자/지도작성자(cartographer) 제라두스 메르카토르(Gerardus Mercator, 1512-1594)에 의해 오늘날 '메르카토르 투영법(Mercator projection)'이라고 부르는 지도 작성법이 소개되고, 보다 정확한 계산을 위해 세칸트 함수의 적분법이 필요하게 되었다. (보다 자세한 내용은 논문 참조: History of the Integral of Secant) 1599년 메르카토르 투영법을 염두에 둔 영국 수학자 에드워드 라이트(Edward Wr..
