| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 적분
- 학년
- a-level
- mathematics
- factor
- differential
- triangle
- equation
- t-치환
- Weierstrass
- DENOMINATOR
- 제도
- 교육
- integral
- Admissions
- Maths
- College
- 영국
- Partial
- Order
- solution
- factors
- GCSE
- Oxford
- algebraic
- division
- 바이어슈트라스
- test
- fractions
- 치환
Archives
- Today
- Total
Cambridge Maths Academy
19. Surface area of a circular cone 본문
수학 모음 (Maths collection)
19. Surface area of a circular cone
Cambridge Maths Academy 2021. 1. 14. 08:50반응형
수학 모음 (Maths collection) 전체보기
To find the surface area of a circular cone, we need to consider the area of the circular sector and the area of the circle.
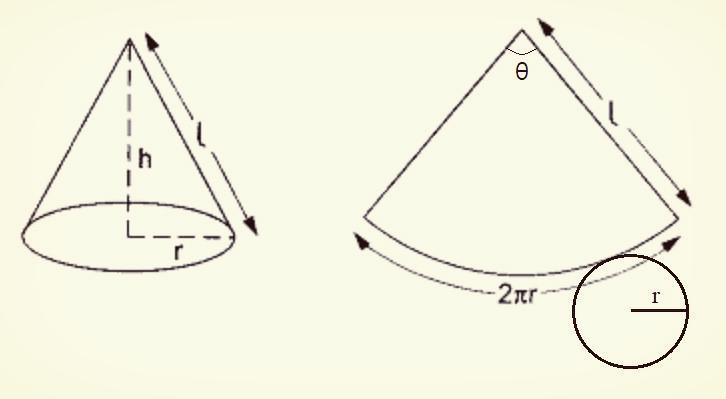
- The area of the circular sector: We find the angle $\theta$ by considering the arc length, i.e. $$ \begin{align} L=2\pi\ell\times\frac{\theta}{360}&=2\pi r \\ \Rightarrow\quad \ell\times\frac{\theta}{360}&=r \end{align} $$ The area is then $$ \begin{align} A_{\rm sector}&=\pi\ell^2\times\frac{\theta}{360} \\ &=\pi\ell\times\underbrace{\left(\ell\times\frac{\theta}{360}\right)}_{r} \\ &=\pi r\ell \end{align} $$
- The area of the circle: $$ \begin{align} A_{\rm circle}=\pi r^2 \end{align} $$
This gives: $$ \begin{align} A&=A_{\rm circle}+A_{\rm sector} \\ &=\pi r^2+\pi r\ell \\ &=\pi r(r+\ell) \qquad\square \end{align} $$
반응형
'수학 모음 (Maths collection)' 카테고리의 다른 글
| 25. Zero's zeroth power is 1 (An interesting observation) (0) | 2021.01.27 |
|---|---|
| 23. Equations vs. Identities (0) | 2021.01.25 |
| 18. Area of regular octagon, n-gon and circle (0) | 2021.01.06 |
| 17. Interest vs Tax rate (0) | 2021.01.05 |
| 8. Heron's formula - Derivation (0) | 2020.06.22 |
Comments


