| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 제도
- solution
- division
- Oxford
- Weierstrass
- fractions
- t-치환
- College
- 영국
- Order
- factor
- 적분
- DENOMINATOR
- differential
- Maths
- 교육
- test
- 학년
- GCSE
- a-level
- 바이어슈트라스
- integral
- triangle
- 치환
- mathematics
- Admissions
- factors
- algebraic
- Partial
- equation
- Today
- Total
목록전체 글 (81)
Cambridge Maths Academy
수학 모음 (Maths collection) 전체보기 Question. Let In=∫sinn(ax)dx (a) Show that In=−1ansinn−1(ax)cos(ax)+n−1nIn−2 Let Jn=∫π20sinnxdx (b) Hence, or otherwise, show that $$ \begin{align} J_n = \frac{n-1}{n}J_{n-2} \end{al..
수학 모음 (Maths collection) 전체보기 Consider J=∫√cotxdxfor0<x≤π2 (a) Method 1. By using the substitution u=√cotx, followed by partial fractions, we can show that $$ \begin{align} J &= \frac1{2\sqrt{2}} \ln \left\vert \frac{1 + \sqrt{2 \cot x} + \cot x}{1 - \sqrt{2 \cot x} + \cot x} \right\..
수학 모음 (Maths collection) 전체보기 Consider I=∫√tanxdxfor0≤x<π2 (a) Method 1. By using the substitution u=√tanx, followed by partial fractions, we can show that $$ \begin{align} I &= \frac1{2\sqrt{2}} \ln \left\vert \frac{ \tan x - \sqrt{2 \tan x} + 1 }{ \tan x + \sqrt{2 \tan x} + 1 } \right..
수학 모음 (Maths collection) 전체보기 Question 1. Given x2+y2=r2, show that dydx=−xyd2ydx2=−r2y3 Solution. 더보기 We use implicit differentiation which is an application of chain rule and product rule as we will see here. $$ \begin{align} && x^2+y^2&=r^2 \\ &\Rightarrow& \frac{{\rm d}}{{\rm d}x} \l..
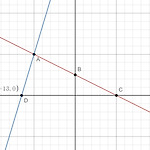 12. Another problem on coordinate geometry (GCSE)
12. Another problem on coordinate geometry (GCSE)
수학 모음 (Maths collection) 전체보기 Question. In the diagram, ABC is the line with equation y=−12x+5 It is also given that AB=BC and that D is the point with coordinates (−13,0). Find an equation of the line through A and D. Solution. B is the y-intercept of y=−12x+5: B=(0,5) C is the x-intercept of $y=-\fr..
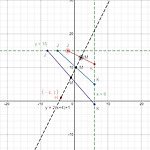 11. A problem on coordinate geometry (GCSE)
11. A problem on coordinate geometry (GCSE)
수학 모음 (Maths collection) 전체보기 Question. Triangle HJK is isosceles with HJ=HK and JK=√80. (i) H is the point with coordinates (−4,1). (ii) J is the point with coordinates (j,15) where j<0. (iii) K is the point with coordinates (6,k). (iv) M is the midpoint of JK. (v) The gradient of HM is 2. Find the value of j and the value of k. Solution. From (i), we can l..
'영국 교육제도와 수학 공부' 전체보기 차례 (Table of contents) A-level 소개 A-level 과목수 A-level 과목수는 많을수록 좋다? A-level 과목 선택 A-level 시험 Exam boards A-level 시험 제도의 변화 (Modular vs Linear) Resit (재시험) 입시 절차 클리어링(Clearing)과 갭이어(Gap year) 1. A-level 소개 A-level은 영국의 의무교육 중 마지막 단계인 Key stage 5(KS5)에 해당하는 과정입니다. (KS5는 크게 '대학 진학을 위한 academic education'과 '직업 교육을 위한 vocational education'으로 나뉩니다. A-level은 academic education을 대표..
'영국 교육제도와 수학 공부' 전체보기 GCSE에서 배우는 수학은 크게 1) Number(수) 2) Algebra(대수) 3) Geometry(기하학) 4) Probability & Statistics(확률과 통계) 이렇게 네 부분으로 나뉘어져 있습니다. 이를 순서대로 배운다기 보다는 각각의 영역을 더 작은 토픽으로 나누어 Number 일부분, Algebra 일부분, Geometry 일부분, Prob & Stats 일부분 이렇게 점진적으로 나아가는 방식으로 진행됩니다. 이는 한국 수학 교과에서도 중1, 중2, 중3의 과정에 이 네 가지 토픽이 적절히 나뉘어져 등장하는 것과 같습니다. '영국 중등교육 GCSE, IGCSE'에서 언급한대로 학습 내용은 한국의 중학과정 ~ 고1 초중반과 비슷합니다. 시험에 출..
