| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- DENOMINATOR
- 제도
- GCSE
- Admissions
- Order
- 바이어슈트라스
- College
- fractions
- equation
- Maths
- Oxford
- division
- solution
- Weierstrass
- mathematics
- differential
- test
- 치환
- a-level
- t-치환
- 적분
- 교육
- 학년
- factors
- 영국
- triangle
- algebraic
- integral
- Partial
- factor
- Today
- Total
Cambridge Maths Academy
11. A problem on coordinate geometry (GCSE) 본문
11. A problem on coordinate geometry (GCSE)
Cambridge Maths Academy 2021. 2. 27. 09:55수학 모음 (Maths collection) 전체보기
Question. Triangle $HJK$ is isosceles with $HJ=HK$ and $JK=\sqrt{80}$.
- (i) $H$ is the point with coordinates $(-4,1)$.
- (ii) $J$ is the point with coordinates $(j,15)$ where $j < 0$.
- (iii) $K$ is the point with coordinates $(6,k)$.
- (iv) $M$ is the midpoint of $JK$.
- (v) The gradient of $HM$ is 2.
Find the value of $j$ and the value of $k$.
Solution.
- From (i), we can locate $H(-4,1)$ exactly.
- From (ii), we know that $J$ is on the straight line $y=15$.
- From (iii), we know that $K$ is on the straight line $x=6$.
- From (v), we know that $M$ is on a line with gradient 2 through $H$. This line has the equation: $$ \begin{align} y-y_1=m(x-x_1) \qquad\Rightarrow\qquad y-1=2(x+4) \end{align} $$.
Based on these, we can draw a diagram:
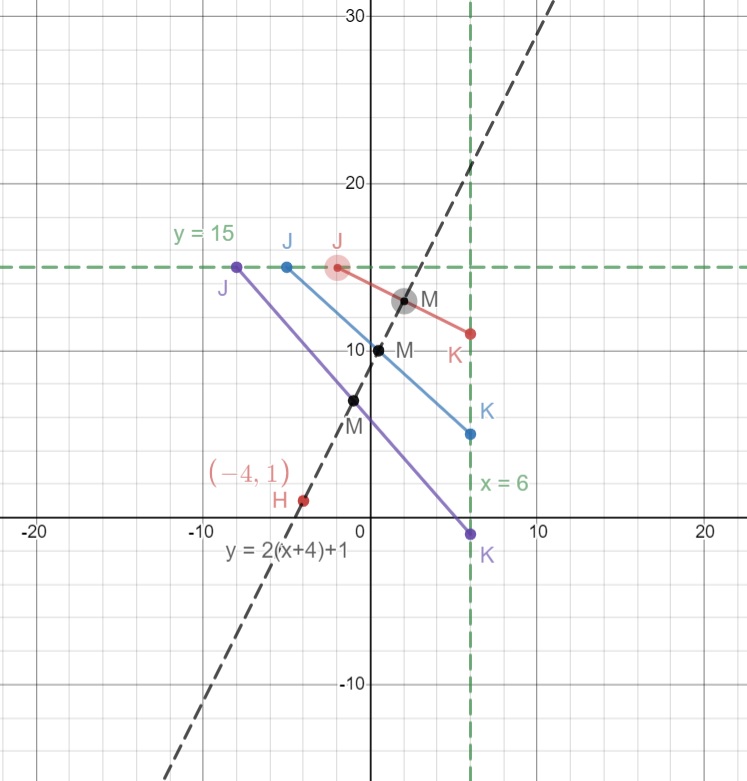
There are many possibilities for $j$ and $k$ with the midpoint $M$ of $JK$ on the line $y=2(x+4)+1$. Our strategy is to find the case where $JK=\sqrt{80}$.
1) Step 1: As $M$ is the midpoint of $JK$, its coordinates are: $$ \begin{align} \left( \frac{j+6}{2},\frac{k+15}{2} \right) \end{align} $$
2) Step 2: The gradient of $HM$ reads: recall $H(-4,1)$ and $M\left( \frac{j+6}{2},\frac{k+15}{2} \right)$, $$ \begin{align} \frac{\Delta y}{\Delta x} &=\frac{\frac{k+15}{2}-1}{\frac{j+6}{2}+4} \\ &=\frac{(k+15)-2}{(j+6)+8} \\ &=\frac{k+13}{j+14} \end{align} $$
It is given that this is equal to 2, i.e. $$ \begin{align} &\Rightarrow& \frac{k+13}{j+14}&=2 \\ &\Rightarrow& k+13&=2(j+14) \\ &\Rightarrow& k&=2j+15 \end{align} $$
3) Step 3: Using $JK=\sqrt{80}$, we find: $$ \begin{align} && JK=\sqrt{(j-6)^2+(15-k)^2}&=\sqrt{80} \\ &\Rightarrow& (j-6)^2+(15-k)^2&=80 \end{align} $$
So we obtain a set of simultaneous equations for $j$ and $k$: $$ \left\{ \begin{array}{l} k=2j+15 \\ (j-6)^2+(15-k)^2=80 \end{array} \right. $$ Substituting the first equation into the second yields: $$ \begin{align} &\Rightarrow& (j-6)^2+(2j)^2&=80 \\ &\Rightarrow& j^2-12j+36+4j^2&=80 \\ &\Rightarrow& 5j^2-12j-44&=0 \\ &\Rightarrow& (j+2)(5j-22)&=0 \\ &\Rightarrow& j=-2\quad{\rm or}\quad j&=\frac{22}{5} \end{align} $$ Since $j < 0$, we find: $$ \begin{align} \therefore\quad j=-2 \qquad{\rm and}\qquad k=11 \end{align} $$
In the diagram below, we see that the two possibilities are subject to the conditions that $M$ is on the line $y=2(x+4)+1$ and $JK=\sqrt{80}$.
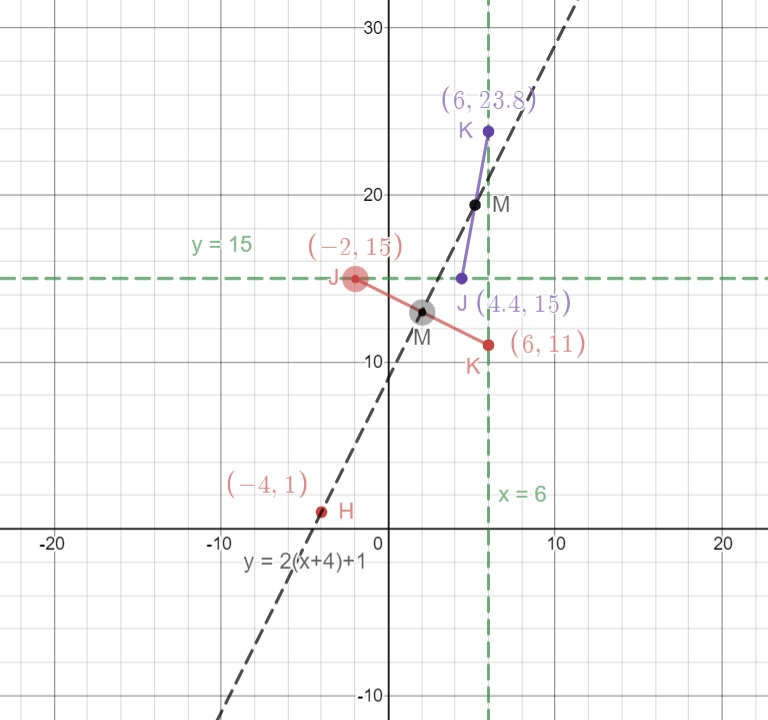
Aside for enthusiasts: It appears that we did not use the condition $HJ=HK$. Let's check whether the answer is consistent with this condition first. With $H(-4,1), J(-2,15)$ and $K(6,11)$, $$ \begin{align} HJ&=\sqrt{(-2+4)^2+(15-1)^2}=\sqrt{2^2+14^2}=\sqrt{4+196}=\sqrt{200} \\ HK&=\sqrt{(6+4)^2+(11-1)^2}=\sqrt{10^2+10^2}=\sqrt{100+100}=\sqrt{200} \end{align} $$ So it is consistent and it means that we have a redundancy in the conditions given in the question - we notice that there are three conditions for two unknowns, $j$ and $k$.
Before we summarise the three conditions, we check what the condition $HJ=HK$ gives: $H(-4,1), J(j,15), K(6,k)$ $$ \begin{align} && d&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\ \\ &\Rightarrow& HJ&=\sqrt{(j+4)^2+(15-1)^2}=\sqrt{(j+4)^2+196} \\ &\Rightarrow& HK&=\sqrt{(6+4)^2+(k-1)^2}=\sqrt{(k-1)^2+100} \end{align} $$ $$ \begin{align} HJ&=HK &&\Rightarrow& (j+4)^2+196&=(k-1)^2+100 \\ &&&\Rightarrow& (j+4)^2-(k-1)^2&=-96 \end{align} $$ Geometrically, $J$ and $K$ would be the intersection points between the circle $(x+4)^2+(y-1)^2=r^2$ and the lines $y=15$ and $x=6$ respectively, where the radius is given by: $$ \begin{align} r^2&=HJ^2=(j+4)^2+196 \\ &=HK^2=(k-1)^2+100 \end{align} $$
The three conditions give: $$ \begin{align} (1)&&& {\rm The \;gradient \;of \;}HM= 2\;:&& k=2j+15 \\ (2)&&& JK=\sqrt{80}\;: && (j-6)^2+(k-15)^2=80 \\ (3)&&& HJ=HK\;: && (j+4)^2-(k-1)^2=-96 \end{align} $$
(i) Method 1: In the solution above, we used (1) and (2).
(ii) Method 2: As an alternative, we can use (1) and (3) in which case we solve the following simultaneous equations: $$ \left\{ \begin{align} (1)&\quad k=2j+15 \\ (3)&\quad (k-1)^2-(j+4)^2=96 \end{align} \right. $$ Substituting (1) into (3) yields: $$ \begin{align} (2j+15-1)^2-(j+4)^2&=96 \\ (2j+14)^2-(j+4)^2&=96 \\ \Big[ (2j+14) + (j+4) \Big] \Big[ (2j+14) - (j+4) \Big]&= 96 \\ (3j+18)(j+10)&=96 \\ 3j^2+48j+180&=96 \\ 3j^2+48j+84&=0 \\ j^2+16j+28&=0 \\ (j+2)(j+14)&=0 \\ j=-2 \quad{\rm or}\quad j&=-14 \end{align} $$ Since they are both negative, we find two possibilities: $$ \begin{align} (j,k)=(-2,11) \qquad{\rm and}\qquad (j,k)=(-14,13) \end{align} $$ However, as we check with the diagram,
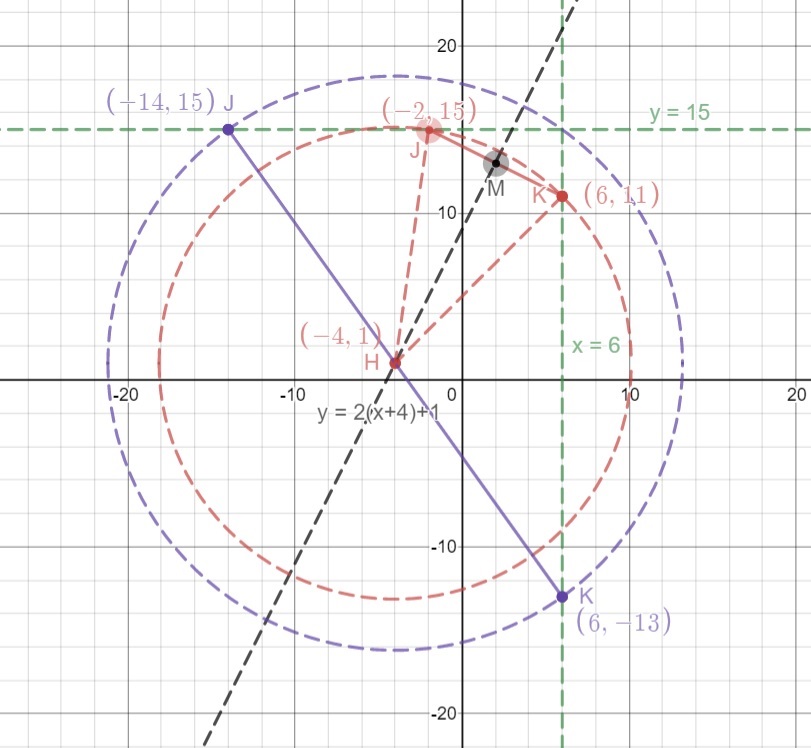
in the case where $j=-14$ (the purple case in the diagram above), $HJK$ does not form a triangle. Hence, we only choose $(j,k)=(-2,11)$.
(iii) Method 3: As a second alternative, we can also use (2) and (3) in which case we solve the following simultaneous equations: $$ \left\{ \begin{align} (2)&\quad (j-6)^2+(k-15)^2=80 \\ (3)&\quad (j+4)^2-(k-1)^2=-96 \end{align} \right. $$ (Note: This is to find the intersection points between a circle and a hyperbola as shown in the diagram below.)
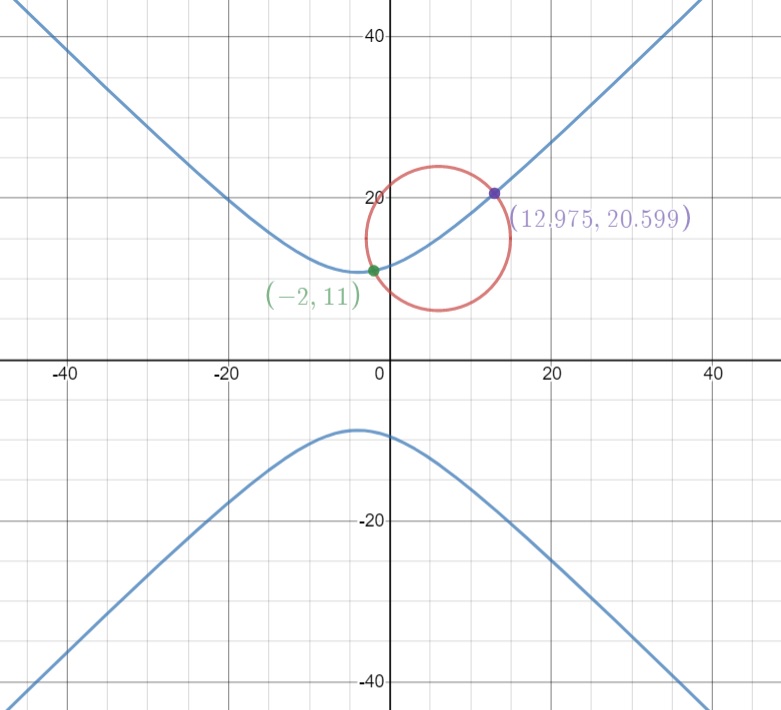
We simplify the two equations: $$ \begin{align} &(2)& (j-6)^2+(k-15)^2&=80 \\ &\Rightarrow& \left(j^2-12j+36\right)+\left(k^2-30k+225\right)&=80 \\ &\Rightarrow& j^2-12j+k^2-30k&=-181 \\ \\ &(3)& (j+4)^2-(k-1)^2&=-96 \\ &\Rightarrow& \left(j^2+8j+16\right)-\left(k^2-2k+1\right)&=-96 \\ &\Rightarrow& j^2+8j-k^2+2k&=-111 \end{align} $$ Adding and subtracting the two equations give: $$ \begin{align} (2)+(3)\;:&& 2j^2-4j-28k&=-292 &&\Rightarrow& j^2-2j-14k&=-146 \\ (2)-(3)\;:&& -20j+2k^2-32k&=-70 &&\Rightarrow& k^2-16k-10j&=-35 \end{align} $$
Using the top equation which says $k=\frac{j^2-2j+146}{14}$ and substituting this into the bottom one, $$ \begin{align} &\Rightarrow&k(k-16)-10j&=-35 \\ &\Rightarrow&\frac{j^2-2j+146}{14}\left(\frac{j^2-2j+146}{14}-16\right)-10j&=-35 \\ &\Rightarrow&\frac{j^2-2j+146}{14}\left(\frac{j^2-2j+146-224}{14}\right)-10j&=-35 \\ &\Rightarrow&\left(j^2-2j+146\right)\left(j^2-2j-78\right)-\underbrace{10\times14^2}_{1960}j&=-\underbrace{13\times14^2}_{6860} \\ &\Rightarrow&\Big[ \left(j^2-2j\right)^2+68\left(j^2-2j\right) - 11388 \Big]-1960j&=-6860 \\ &\Rightarrow&\left(j^4-4j^3+4j^2\right)+68\left(j^2-2j\right)-1960j-4528&=0 \\ &\Rightarrow&j^4-4j^3+72j^2-2096j-4528&=0 \\ &\Rightarrow&(j+2)\left( j^3-6j^2+84j-2264 \right)&=0 \\ &\Rightarrow& j=-2 \quad{\rm or}\quad j&\approx 12.975 \end{align} $$ Since $j < 0$, we choose $j=-2$ and it gives $k=11$.
For completeness, the cubic equation $j^3-6j^2+84j-2264=0$ has the following roots: $$ \begin{align} j_1&= 2 \left( 1- \frac{6^{\frac23}}{\sqrt[3]{22+7\sqrt{10}}} + \sqrt[3]{6\left( 22+7\sqrt{10}\right)} \right) \approx 12.975 \\ j_2&= 2 \left( 1 + \frac{6^{\frac23}{\rm e}^{-\frac{i\pi}{3}}}{\sqrt[3]{22+7\sqrt{10}}} - {\rm e}^{\frac{i\pi}{3}}\sqrt[3]{6\left( 22+7\sqrt{10} \right)} \right) \\ j_3&= 2 \left( 1 + \frac{6^{\frac23}{\rm e}^{\frac{i\pi}{3}}}{\sqrt[3]{22+7\sqrt{10}}} - {\rm e}^{-\frac{i\pi}{3}}\sqrt[3]{6\left( 22+7\sqrt{10} \right)} \right) \end{align} $$
The two possibilities $$ \begin{align} (j,k)=(-2,11) \qquad{\rm and}\qquad (j,k)=(12.975,20.599) \end{align} $$ correspond to the following diagram with $HJ=HK$ and $JK=\sqrt{80}$.

'수학 모음 (Maths collection) > Technical B - Problem solving' 카테고리의 다른 글
| 13. Implicit differentiation and the second order derivatives (0) | 2021.03.03 |
|---|---|
| 10. A challenging geometry question (STEP level) (0) | 2021.01.26 |
| 9. Three cards with an even score (GCSE) (0) | 2021.01.14 |
| 8. Some integrals (0) | 2020.12.31 |
| 7. Differentiation - Some inverse trigonometric functions (0) | 2020.12.31 |