| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 제도
- algebraic
- 치환
- test
- factor
- equation
- 교육
- 바이어슈트라스
- differential
- Weierstrass
- fractions
- 적분
- Admissions
- Maths
- a-level
- factors
- t-치환
- College
- 학년
- division
- DENOMINATOR
- GCSE
- triangle
- Order
- solution
- integral
- mathematics
- Partial
- 영국
- Oxford
- Today
- Total
Cambridge Maths Academy
17. Interest vs Tax rate 본문
수학 모음 (Maths collection) 전체보기
Question. Misha invests £4000 in a bank with a compound interest rate of 3.75% per annum.
At the end of each year Misha has to pay 20% tax on the interest made during that year.
After 4 years Misha finds a ruby stone valued at 4500. Has he go enough money in the bank to afford to buy the ruby stone? If not, how much more would he need to save?
Solution. For GCSE/middle-school students, we may calculate the total year by year.
- At the end of the 1st year: $$ \begin{align} {\rm Interest\;}:&\qquad 4000\times\frac{3.75}{100}=150 \\ {\rm Tax\;}:&\qquad 150\times\frac{20}{100}=30 \\ {\rm Total\;}:&\qquad A_1=4000+150-30=4120 \end{align} $$
- At the end of the 2nd year: $$ \begin{align} {\rm Interest\;}:&\qquad 4120\times\frac{3.75}{100}=154.5 \\ {\rm Tax\;}:&\qquad 150\times\frac{20}{100}=30.9 \\ {\rm Total\;}:&\qquad A_2=4120+154.5-30.9=4243.6 \end{align} $$
- At the end of the 3rd year: $$ \begin{align} {\rm Interest\;}:&\qquad 4243.6\times\frac{3.75}{100}=159.135 \\ {\rm Tax\;}:&\qquad 159.135\times\frac{20}{100}=31.827 \\ {\rm Total\;}:&\qquad A_3=4243.6+159.135-31.827=4370.908 \end{align} $$
- At the end of the 4th year: $$ \begin{align} {\rm Interest\;}:&\qquad 4370.908\times\frac{3.75}{100}=163.90905 \\ {\rm Tax\;}:&\qquad 163.90905\times\frac{20}{100}=32.78181 \\ {\rm Total\;}:&\qquad A_4=4370.908+163.90905-32.78181=4502.03524 \end{align} $$
Thus, Misha has enough money by 2.04 pounds.
Alternative. For more advanced students, we may formulate this slightly more efficiently. To do this, let's recall how we approach the interest problems in general which leads to a geometric sequence.
A recapitulation. For an initial amount $a$ with an annual compound interest rate of $r$%, we find
$$ \begin{align} {\rm 1st\;year\;:}&\qquad A_1=a+a\times\frac{r}{100}=a\left(1+\frac{r}{100}\right) \\ {\rm 2nd\;year\;:}&\qquad A_2=A_1+A_1\times\frac{r}{100}=A_1\left(1+\frac{r}{100}\right)=a\left(1+\frac{r}{100}\right)^2 \\ {\rm 3rd\;year\;:}&\qquad A_3=A_2+A_2\times\frac{r}{100}=A_2\left(1+\frac{r}{100}\right)=a\left(1+\frac{r}{100}\right)^3 \\ &\;\vdots \\ n{\rm -th\;year\;:}&\qquad A_n=a\left(1+\frac{r}{100}\right)^n \end{align} $$
With a tax rate $t$% on the interest, we find $$ \begin{align} {\rm 1st\;year\;:}&\qquad A_1=a+a\times\frac{r}{100}-a\times\frac{r}{100}\times\frac{t}{100}=a\left(1+\frac{r}{100}-\frac{rt}{10000}\right) \\ {\rm 2nd\;year\;:}&\qquad A_2=A_1\left(1+\frac{r}{100}-\frac{rt}{10000}\right)=a\left(1+\frac{r}{100}-\frac{rt}{10000}\right)^2 \\ {\rm 3rd\;year\;:}&\qquad A_3=A_2\left(1+\frac{r}{100}-\frac{rt}{10000}\right)=a\left(1+\frac{r}{100}-\frac{rt}{10000}\right)^3 \\ &\;\vdots \\ n{\rm -th\;year\;:}&\qquad A_n=a\left(1+\frac{r}{100}-\frac{rt}{10000}\right)^n \end{align} $$
Application. As we apply this formula to the question above with $r=3.75$ and $t=20$, we find $$ \begin{align} {\rm 1st\;year\;:}&\qquad A_1=a\left(1+\frac{r}{100}-\frac{rt}{10000}\right)=4000\left(1+\frac{3.75}{100}-\frac{3.75\times20}{10000}\right)=4120 \\ {\rm 2nd\;year\;:}&\qquad A_2=a\left(1+\frac{r}{100}-\frac{rt}{10000}\right)^2=4000\left(1+\frac{3.75}{100}-\frac{3.75\times20}{10000}\right)^2=4243.6 \\ {\rm 3rd\;year\;:}&\qquad A_3=a\left(1+\frac{r}{100}-\frac{rt}{10000}\right)^3=4000\left(1+\frac{3.75}{100}-\frac{3.75\times20}{10000}\right)^3=4370.908 \\ {\rm 4th\;year\;:}&\qquad A_4=a\left(1+\frac{r}{100}-\frac{rt}{10000}\right)^4=4000\left(1+\frac{3.75}{100}-\frac{3.75\times20}{10000}\right)^4=4502.03524 \end{align} $$ which agree with the values obtained in the solution above.
A further investigation for enthusiasts. There is a balance between interest and tax rates. Recall
$$ \begin{align} A_n=a\left(1+\frac{r}{100}-\frac{rt}{10000}\right)^n \end{align} $$ If we pay too much tax, then $A_n$ may become less than the original amount $a$ in which case people won't be so happy. So the government would determine the tax rate $t$ such that $A_n\ge a$. Let $$ \begin{align} x&=\frac{r}{100} \\ y&=\frac{t}{100} \end{align} $$ then we have $$ \begin{align} A_n=a\left(1+x-xy\right)^n&\ge a \\ \Rightarrow\quad 1+x-xy&\ge 1 \end{align} $$ It gives $$ \begin{align} x\underbrace{(1-y)}_{0\le\quad\le 1}&\ge 0 &&{\rm and} & xy&\le x \\ \\ \Rightarrow\quad x&\ge0 &&{\rm and}& y&\le 1 \end{align} $$ So, as long as we have a positive interest rate and $t<100\%$, the sum increases. This is because the tax is paid only for the interest.
Another investigation for enthusiasts. Suppose that tax is paid for the total amount, i.e.
$$ \begin{align} {\rm 1st\;year\;:}&\qquad A_1=a+a\times\frac{r}{100}-a\left(1+\times\frac{r}{100}\right)\frac{t}{100}=a\left(1+\frac{r}{100}\right)\left(1-\frac{rt}{10000}\right) \\ {\rm 2nd\;year\;:}&\qquad A_2=A_1\left(1+\frac{r}{100}\right)\left(1-\frac{rt}{10000}\right)=a\left(1+\frac{r}{100}\right)^2\left(1-\frac{rt}{10000}\right)^2 \\ {\rm 3rd\;year\;:}&\qquad A_3=A_2\left(1+\frac{r}{100}\right)\left(1-\frac{rt}{10000}\right)=a\left(1+\frac{r}{100}\right)^3\left(1-\frac{rt}{10000}\right)^3 \\ &\;\vdots \\ n{\rm -th\;year\;:}&\qquad A_n=a\left(1+\frac{r}{100}\right)^n\left(1-\frac{rt}{10000}\right)^n \end{align} $$ As before, let $$ \begin{align} x&=\frac{r}{100} \\ y&=\frac{t}{100}. \end{align} $$ then $$ \begin{align} A_n=a(1+x)^n(1-y)^n \end{align} $$ In order for $A_n\ge a$, we need $$ \begin{align} (1+x)(1-y)\ge 1 \end{align} $$ which gives $$ \begin{align} 1+x&\ge\frac1{1-y} &&{\rm and} & 1-y&\ge\frac1{1+x} \\ \Rightarrow\quad x&\ge-1-\frac1{y-1} &&{\rm and}& y&\le 1-\frac1{x+1} \end{align} $$ By sketching the curves,
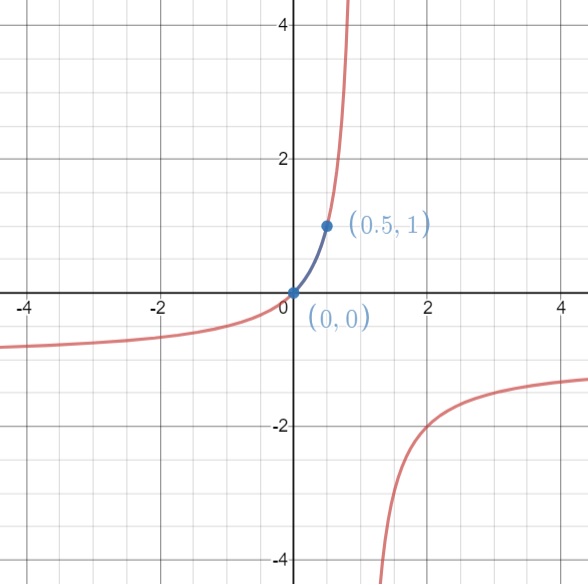
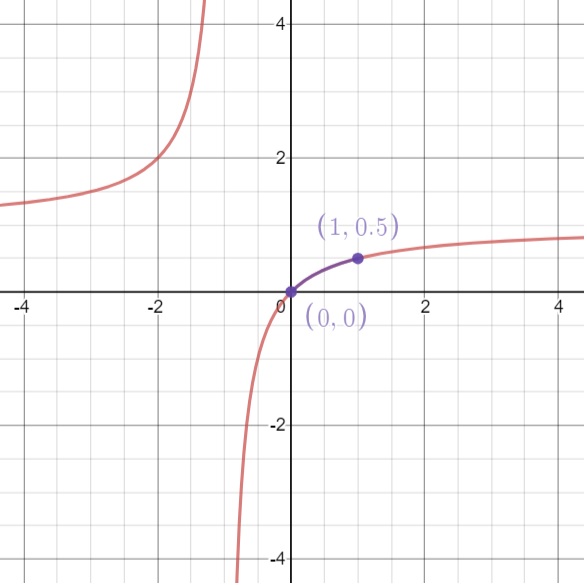
we find $$ \begin{align} 0\le x \le 1 \qquad{\rm and}\qquad 0\le y\le \frac12 \end{align} $$ So the tax rate cannot be more than 50%. Otherwise, we lose money. It is interesting to quote a few values so as to keep the same amount of money.
| Interest rate $r$% | Tax rate $t$% |
| 10% | 9.1% |
| 20% | 16.7% |
| 30% | 23.1% |
| 40% | 28.6% |
| 50% | 33.3% |
| 60% | 37.5% |
| 70% | 41.2% |
| 80% | 44.4% |
| 90% | 47.4% |
| 100% | 50% |
'수학 모음 (Maths collection)' 카테고리의 다른 글
| 25. Zero's zeroth power is 1 (An interesting observation) (0) | 2021.01.27 |
|---|---|
| 23. Equations vs. Identities (0) | 2021.01.25 |
| 19. Surface area of a circular cone (0) | 2021.01.14 |
| 18. Area of regular octagon, n-gon and circle (0) | 2021.01.06 |
| 8. Heron's formula - Derivation (0) | 2020.06.22 |