18. Area of regular octagon, n-gon and circle

수학 모음 (Maths collection) 전체보기

 

1. Area of a regular octagon

 

Question. Find the area of a regular octagon with side length $a$.

 

(4-9 Higher GCSE by Michael White, Ch13 Geometry 4, p.426 Q19.)

 

 

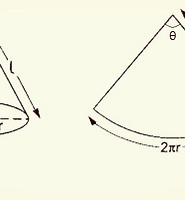
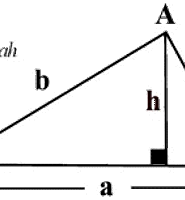
We consider the area of the triangle with an angle $\theta$ subtended at the centre.

 

 

$$\begin{align} \theta=\frac{360}{8}=45^\circ \end{align}$$ The height $h$ of the triangle is given by $$\begin{align} \tan\frac{\theta}{2}=\frac{a/2}{h} \qquad\Rightarrow\qquad h=\frac{a/2}{\tan\frac{\theta}{2}} \end{align}$$ Then, the area of the triangle is given by $$\begin{align} T&=\frac12\times a\times h \\ &=\frac12\frac{\frac{a^2}{2}}{\tan\frac{\theta}{2}} \\ &=\frac{\left(\frac{a}{2}\right)^2}{\tan\frac{\theta}{2}} \\ &=\frac{\left(\frac{a}{2}\right)^2}{\tan22.5^\circ} \\ &=\frac{\left(\frac{a}{2}\right)^2}{\sqrt{2}-1} \\ &=\frac{a^2\left(\sqrt{2}+1\right)}{4} \end{align}$$ There are 8 such triangles in octagon and its area thus reads $$\begin{align} A_8=8T=2\left(\sqrt{2}+1\right)a^2 \end{align}$$

 

2. Area of a regular $n$-gon

 

We can generalise the result above to a regular $n$-gon. The angle subtended at the centre is $$\begin{align} \theta=\frac{360}{n} \end{align}$$ The area of a triangle is given by $$\begin{align} T=\frac{\left(\frac{a}{2}\right)^2}{\tan\frac{\theta}{2}} =\frac{\left(\frac{a}{2}\right)^2}{\tan\frac{180}{n}} \end{align}$$ There are $n$ such triangles in a regular $n$-gon and its area thus reads $$\begin{align} A_n=nT=\frac{n\left(\frac{a}{2}\right)^2}{\tan\frac{180}{n}}=\frac{n\left(\frac{a}{2}\right)^2}{\tan\frac{\pi}{n}} \end{align}$$ We can check this formula for a few values of $n$. $$\begin{align} A_3&=\frac{3\left(\frac{a}{2}\right)^2}{\tan60^\circ}=\frac{3\left(\frac{a}{2}\right)^2}{\tan\frac{\pi}{3}}=\frac{\sqrt{3}}{4}a^2 \\ A_4&=\frac{4\left(\frac{a}{2}\right)^2}{\tan45^\circ}=\frac{3\left(\frac{a}{2}\right)^2}{\tan\frac{\pi}{4}}=a^2 \\ A_5&=\frac{5\left(\frac{a}{2}\right)^2}{\tan36^\circ}=\frac{3\left(\frac{a}{2}\right)^2}{\tan\frac{\pi}{5}}=\frac{5a^2}{4\sqrt{5-2\sqrt{5}}}=\frac{\sqrt{5\left(5+2\sqrt{5}\right)}}{4}a^2 \\ A_6&=\frac{6\left(\frac{a}{2}\right)^2}{\tan30^\circ}=\frac{3\left(\frac{a}{2}\right)^2}{\tan\frac{\pi}{6}}=\frac{3\sqrt{3}}{2}a^2 \\ A_8&=\frac{8\left(\frac{a}{2}\right)^2}{\tan22.5^\circ}=\frac{3\left(\frac{a}{2}\right)^2}{\tan\frac{\pi}{8}}=\frac{2a^2}{\sqrt{2}-1}=2\left(\sqrt{2}+1\right)a^2 \end{align}$$

 

3. Circle as a regular $\infty$-gon

 

We may view a circle as a regular polygon with an infinite number of sides. Recall $$\begin{align} A_n=\frac{n\left(\frac{a}{2}\right)^2}{\tan\frac{\pi}{n}} \end{align}$$ where the angle is measured in radians. As $n\rightarrow\infty$, the angle $\frac{\pi}{n}$ becomes small and we have (e.g. by Maclaurin/Taylor expansion) $$\begin{align} \tan\frac{\pi}{n}\simeq\frac{\pi}{n} \end{align}$$ Also, the side length is given by $$\begin{align} a=\frac{\ell}{n} \end{align}$$ where $\ell$ is the perimeter. The area then reads $$\begin{align} A_\infty &=\lim_{n\rightarrow\infty}\frac{n\left(\frac{a}{2}\right)^2}{\tan\frac{\pi}{n}} \\ &=\lim_{n\rightarrow\infty}\frac{n\left(\frac{\ell}{2n}\right)^2}{\tan\frac{\pi}{n}} \\ &=\lim_{n\rightarrow\infty}\frac{\frac{\ell^2}{4n}}{\frac{\pi}{n}} \\ &=\frac{\ell^2}{4\pi} \end{align}$$

For $\ell=2\pi r$, it gives $$\begin{align} A_\infty=\frac{(2\pi r)^2}{4\pi}=\pi r^2\quad\checkmark \end{align}$$