| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- mathematics
- triangle
- fractions
- equation
- 학년
- factors
- test
- differential
- Oxford
- 치환
- 적분
- division
- t-치환
- College
- DENOMINATOR
- 교육
- 제도
- Partial
- a-level
- factor
- 바이어슈트라스
- 영국
- Maths
- GCSE
- Weierstrass
- solution
- Order
- integral
- Admissions
- algebraic
- Today
- Total
Cambridge Maths Academy
8. Heron's formula - Derivation 본문
수학 모음 (Maths collection) 전체보기
Heron's formula calculates the area of a triangle. Here, we will look at two different formulae describing the area of a triangle and then derive the third version, Heron's formula.
- $A=\frac12ah$
- $A=\frac12ab\sin C$
- Heron's formula: $A=\sqrt{s(s-a)(s-b)(s-c)}\,$ where $s=\frac{a+b+c}{2}$. s can be thought of as half the perimeter of the triangle.
As we will see, they are all equivalent and therefore can be used interchangeably depending on the available conditions.
Area of a triangle 1
As widely known, the area of a triangle is:

$$ {\rm Area}=\frac12\times{\rm base}\times{\rm height}=\frac12ah$$
Area of a triangle 2: Trigonometry
We can express the height h in terms of b and the angle C using trigonometry, i.e. $h=b\sin C$
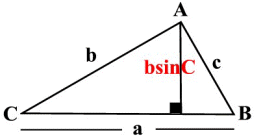
$$ A=\frac12ah=\frac12ab\sin C$$
Comment: This formula can be used when two sides and the angle between them are known.
The cosine rule
In order to derive Heron's formula, we need to recall what's commonly called the cosine rule:
$$ \begin{align} a^2&=b^2+c^2-2bc\cos A &&\Leftrightarrow& \cos A&=\frac{b^2+c^2-a^2}{2bc} \\ b^2&=c^2+a^2-2ca\cos B &&\Leftrightarrow& \cos B&=\frac{c^2+a^2-b^2}{2ca} \\ c^2&=a^2+b^2-2ab\cos C &&\Leftrightarrow& \cos C&=\frac{a^2+b^2-c^2}{2ab} \end{align} $$
- The left hand column says 'a length of a triangle can be expressed in terms of the other two lengths and the angle betweem them'.
- The right hand column says 'each angle can be expressed in terms of three lengths'.
Proof. The cosine rule can be proved by Pythagoras' theorem.

There are two right-angled triangles in the diagram such that their bases are x and y respectively. Pythagoras' theorem applied to them yield:
$$ \begin{align} {\rm Left-hand\;\triangle}:\qquad x^2+h^2&=b^2 \\ {\rm Right-hand\;\triangle}:\qquad y^2+h^2&=c^2 \\ \Rightarrow\qquad y^2-x^2&=c^2-b^2 \end{align} $$
Note that $y=a-x$ and $x=b\cos C$, $$ \begin{align} c^2&=b^2+y^2-x^2 \\ &=b^2+(a-x)^2-x^2 \\ &=b^2+a^2-2ax+x^2-x^2 \\ &=a^2+b^2-2ab\cos C\qquad\square \end{align} $$
Area of a triangle 3: Heron's formula
$$ A=\sqrt{s(s-a)(s-b)(s-c)},\qquad s=\frac{a+b+c}2 $$
Using the cosine rule, we can derive Heron's formula from the second version of the area of a triangle:
$$ \begin{align} A&=\frac12ab\sin C \\ &=\frac12ab\sqrt{1-\cos^2C}\quad{\rm since}\quad \cos^2C+\sin^2C=1 \\ &=\frac12ab\sqrt{1-\left(\frac{a^2+b^2-c^2}{2ab}\right)^2} \\ &=\frac12ab\sqrt{1-\frac{\left(a^2+b^2-c^2\right)^2}{4a^2b^2}} \\ &=\frac14\sqrt{(2ab)^2-\left(a^2+b^2-c^2\right)^2} \\ &=\frac14\sqrt{\left(2ab+a^2+b^2-c^2\right)\left(2ab-a^2-b^2+c^2\right)} \\ &=\frac14\sqrt{\left[(a+b)^2-c^2\right]\left[c^2-(a-b)^2\right]} \\ &=\frac14\sqrt{(a+b+c)(a+b-c)(c+a-b)(c-a+b)} \\ &=\sqrt{\left(\frac{a+b+c}2\right)\left(\frac{a+b-c}2\right)\left(\frac{c+a-b}2\right)\left(\frac{c-a+b}2\right)} \\ &=\sqrt{\left(\frac{a+b+c}2\right)\left(\frac{a+b+c-2c}2\right)\left(\frac{c+a+b-2b}2\right)\left(\frac{c+a+b-2a}2\right)} \\ &=\sqrt{\left(\frac{a+b+c}2\right)\left(\frac{a+b+c}2-c\right)\left(\frac{c+a+b}2-b\right)\left(\frac{c+a+b}2-a\right)} \\ &=\sqrt{s(s-a)(s-b)(s-c)} \qquad\square \end{align}$$
Comment: Heron's formula can be used when three sides (and no angles) of a triangle are known. To remind you, while this is a convenient formula as long as one remembers its form, one can always work out one of the angles using the cosine rule and then use $\frac12ab\sin C$. Heron's formula only provides a short-cut.
'수학 모음 (Maths collection)' 카테고리의 다른 글
| 25. Zero's zeroth power is 1 (An interesting observation) (0) | 2021.01.27 |
|---|---|
| 23. Equations vs. Identities (0) | 2021.01.25 |
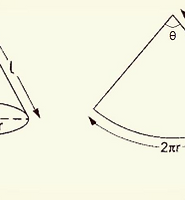
| 19. Surface area of a circular cone (0) | 2021.01.14 |
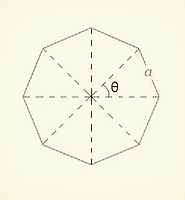
| 18. Area of regular octagon, n-gon and circle (0) | 2021.01.06 |
| 17. Interest vs Tax rate (0) | 2021.01.05 |