| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- a-level
- mathematics
- Maths
- College
- solution
- division
- factor
- test
- Admissions
- GCSE
- algebraic
- t-치환
- 제도
- Partial
- differential
- 바이어슈트라스
- integral
- Weierstrass
- 영국
- triangle
- 적분
- Oxford
- 치환
- fractions
- factors
- DENOMINATOR
- equation
- Order
- 학년
- 교육
- Today
- Total
Cambridge Maths Academy
2. 시컨트/세칸트(sec x)의 적분법 | Integration of sec x 본문
2. 시컨트/세칸트(sec x)의 적분법 | Integration of sec x
Cambridge Maths Academy 2020. 6. 6. 23:20수학 모음 (Maths collection) 전체보기
0. 역사적 배경
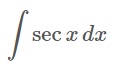
시컨트/세칸트 함수 적분의 역사는 16세기 말~17세기 초, 항해(sea navigation)와 그에 필요한 지도 제작 시기로 거슬러 올라간다.
1569년 벨기에 지도학자/지도작성자(cartographer) 제라두스 메르카토르(Gerardus Mercator, 1512-1594)에 의해 오늘날 '메르카토르 투영법(Mercator projection)'이라고 부르는 지도 작성법이 소개되고, 보다 정확한 계산을 위해 세칸트 함수의 적분법이 필요하게 되었다. (보다 자세한 내용은 논문 참조: History of the Integral of Secant)
1599년 메르카토르 투영법을 염두에 둔 영국 수학자 에드워드 라이트(Edward Wright, 1561-1615)는 수치적 방법으로 이 적분값을 구하게 된다.
1614년 스코틀랜드 수학자 존 네이피어(John Napier, 1550-1617)는 역사상 처음으로 로그표를 발표하고, 1620년 영국 수학자 에드먼드 건터(Edmund Gunter, 1581-1626)는 탄젠트의 로그값(log-tan) 표를 만들게 된다. (네이피어의 책은 라이트(Edward Wright)에 의해 『A Description of the Admirable Table of Logarithms』로 번역되어 1616년 출판되고, 건터(Edmund Gunter)의 탄젠트-로그값은 그의 1620년 저서 『Canon Triangulorum』에 출판된다.)
런던의 항해 선생이었던 헨리 본드(Henry Bond, c. 1600-1678)는 1640년대에 접어들어 라이트(Wright)의 수치적 값과 건터(Gunter)의 탄젠트 로그값을 비교하는 와중에 다음 결과
$$ \int\sec x\,\textrm{d}x=\ln\left\vert\tan\left(\frac{x}{2}+\frac{\pi}{4}\right)\right\vert $$
를 추측하게 된다. 이후 이 결과의 수학적 증명은 학계의 과제가 되고, 1665년경 중력의 발견자이자 미적분의 창시자 아이작 뉴턴(Isaac Newton, 1642-1727)도 이 결과를 알고 있었던 것으로 전해진다.
이 결과를 포함하여 시컨트/세칸트의 적분을 다음과 같이 4가지 방법으로 유도해보자.
$$ \begin{align} \int\sec x\,\textrm{d}x&=\ln\vert\sec x+\tan x\vert+c \\ &=\frac12\ln\left\vert\frac{1+\sin x}{1-\sin x}\right\vert+c \\ &=\ln\left\vert\frac{1+\tan\frac{x}2}{1-\tan\frac{x}2}\right\vert+c \\ &=\ln\left\vert\tan\left(\frac{x}2+\frac{\pi}4\right)\right\vert+c \end{align} $$
1. $u=\sec x+\tan x$ 치환적분
$$ \int\sec x\,\textrm{d}x=\ln\vert\sec x+\tan x\vert+c $$
이 결과는 스코틀랜드 수학자 제임스 그레고리(James Gregory, 1638 - 1675)가 그의 1668년 저서 『Exercitationes Geometricae (Geometrical exercises)』에 소개한 것으로 전해지고, 교과서에 가장 많이 등장하는 표준 결과이기도 하다. ('A brief history of $\pi$'에도 등장하는 그 그레고리다.)
그러나 설명은 대개 '우변을 미분하면 좌변이 나온다'에 그치기 때문에 결과를 '유도(derive)'한다기 보다 '답을 알고 끼워맞춘 것 아닐까'하는 인상을 받게 된다.
이 방법은 삼각함수의 미적분 중 다음 두 가지 결과를 사용한다.
$$ \begin{align} \frac{\textrm{d}}{\textrm{d}x}\tan x&=\sec^2x &&\Rightarrow& \int\sec^2x\,\textrm{d}x&=\tan x+c \\ \frac{\textrm{d}}{\textrm{d}x}\sec x&=\sec x\tan x &&\Rightarrow& \int\sec x\tan x\,\textrm{d}x&=\sec x+c \end{align} $$
이제 적분을 전개하면,
$$ \begin{align} I&=\int\sec x\,\textrm{d}x \\ &=\int\frac{\sec x(\sec x+\tan x)}{\sec x+\tan x}\,\textrm{d}x \\ &=\int\frac{\sec^2x+\sec x\tan x}{\sec x+\tan x}\,\textrm{d}x \end{align} $$
분자가 분모의 도함수라는 것이 보이면 바로 자연로그로 적분 가능하고, $u=\sec x+\tan x$로 치환하면 이 과정을 자세히 볼 수 있다.
$$ \begin{align} u&=\sec x+\tan x \\ \textrm{d}u&=\sec x\tan x+\sec^2x \end{align}$$
$$ \begin{align} \Rightarrow \quad I&=\int\frac{\sec^2x+\sec x\tan x}{\sec x+\tan x}\,\textrm{d}x \\ &=\int\frac{\textrm{d}u}{u} \\ &=\ln\vert u\vert+c \\ &=\ln\vert\sec x+\tan x\vert+c \qquad \square \end{align} $$
2. $u=\sin x$ 치환과 부분분수(partial fractions)
$$ \int\sec x\,\textrm{d}x=\frac12\ln\left\vert\frac{1+\sin x}{1-\sin x}\right\vert+c $$
이는 역사적으로 처음 등장한 시컨트/세칸트의 '체계적' 적분법으로, 뉴턴의 지도교수였던 아이작 배로우(Isaac Barrow, 1630-1677)에 의해 발견되었다. 배로우의 이 방법은 적분에 부분분수(partial fractions)를 처음 도용한 예이기도 하다. 배로우는 자신의 1670년 저서 『Geometrical Lectures』에서 이 방법을 소개하였다. (참고로 2022년 2월 5일 기준, 구글 검색을 통해 이 책의 pdf파일을 구할 수 있다.)
$$ \begin{align} \int\sec x\,\textrm{d}x&=\int\frac1{\cos x}\,\textrm{d}x \\ &=\int\frac{\cos x}{\cos^2x}\,\textrm{d}x \\ &=\int\frac{\cos x}{1-\sin^2x}\,\textrm{d}x \qquad (u=\sin x,\quad \textrm{d}u=\cos x\,\textrm{d}x) \\ &=\int\frac{\textrm{d}u}{1-u^2} \\ &=\int\frac1{(1+u)(1-u)}\,\textrm{d}u \\ &=\int\frac12\left(\frac1{1+u}+\frac1{1-u}\right)\,\textrm{d}u \qquad (부분분수의 활용) \\ &=\frac12\Big[\ln\vert1+u\vert-\ln\vert1-u\vert\Big]+c \\ &=\frac12\ln\left\vert\frac{1+u}{1-u}\right\vert+c \\ &=\frac12\ln\left\vert\frac{1+\sin x}{1-\sin x}\right\vert+c \qquad \square \end{align} $$
Check: 앞서 방법1에서 도출한 결과와 동일함도 확인할 수 있다.
$$ \begin{align} I&=\frac12\ln\left\vert\frac{1+\sin x}{1-\sin x}\right\vert+c \\ &=\frac12\ln\left\vert\frac{1+\sin x}{1-\sin x}\cdot\frac{1+\sin x}{1+\sin x}\right\vert+c \\ &=\frac12\ln\left\vert\frac{(1+\sin x)^2}{1-\sin^2x}\right\vert+c \\ &=\frac12\ln\left\vert\frac{(1+\sin x)^2}{(\cos x)^2}\right\vert+c \\ &=\ln\left\vert\frac{1+\sin x}{\cos x}\right\vert+c \\ &=\ln\vert\sec x+\tan x\vert+c \qquad \square \end{align} $$
3. $t=\tan\frac{x}2$ 치환 (t-치환 또는 바이어슈트라스 치환)
$$ \int\sec x\,\textrm{d}x=\ln\left\vert\frac{1+\tan\frac{x}2}{1-\tan\frac{x}2}\right\vert+c
$$
시컨트와 코시컨트 적분은 t-치환 또는 바이어슈트라스 치환(Weierstrass substitution)의 대표적인 예이기도 하다. t-치환의 핵심은 $t=\tan\frac{x}2\,$을 사용하여 $\textrm{d}x$, $\cos x\,$와 $\sin x\,$를 모두 t를 사용한 분수(유리함수)로 나타낼 수 있다는 데 있다.
$$ \begin{align} && t&=\tan\frac{x}2 \\ &\Rightarrow& \textrm{d}t&=\frac12\underbrace{\sec^2\frac{x}2}_{1+\tan^2\frac{x}2}\,\textrm{d}x=\frac{1+\tan^2\frac{x}2}2\,\textrm{d}x=\frac{1+t^2}2\,\textrm{d}x \\ &\Rightarrow& \textrm{d}x&=\frac{2}{1+t^2}\,\textrm{d}t \\ \\ && \cos x&=\cos^2\frac{x}2-\sin^2\frac{x}2=\cos^2\frac{x}2\left(1-\tan^2\frac{x}2\right)=\frac{1-\tan^2\frac{x}2}{\sec^2\frac{x}2}=\frac{1-\tan^2\frac{x}2}{1+\tan^2\frac{x}2}=\frac{1-t^2}{1+t^2} \\ && \sin x&=2\sin\frac{x}2\cos\frac{x}2=2\cos^2\frac{x}2\tan\frac{x}2=\frac{2\tan\frac{x}2}{\sec^2\frac{x}2}=\frac{2\tan\frac{x}2}{1+\tan^2\frac{x}2}=\frac{2t}{1+t^2} \end{align} $$
이제 시컨트/세칸트 적분에 적용하면,
$$ \begin{align} \int\sec x\,\textrm{d}x &=\int\frac1{\cos x}\,\textrm{d}x \\ &=\int\frac1{\frac{1-t^2}{1+t^2}}\frac{2}{1+t^2}\,\textrm{d}t \\ &=\int\frac2{1-t^2}\,\textrm{d}t \\ &=\int\frac2{(1+t)(1-t)}\,\textrm{d}t \\ &=\int\left(\frac1{1+t}+\frac1{1-t}\right)\,\textrm{d}t \qquad (부분분수의 활용) \\ &=\ln\vert1+t\vert-\ln\vert1-t\vert+c \\ &=\ln\left\vert\frac{1+t}{1-t}\right\vert+c \\ &=\ln\left\vert\frac{1+\tan\frac{x}2}{1-\tan\frac{x}2}\right\vert+c \qquad \square \end{align} $$
Check 1: 방법2에서 얻은 결과로부터 방법3의 결과를 도출할 수 있다.
$$ \begin{align} I&=\frac12\ln\left\vert\frac{1+\sin x}{1-\sin x}\right\vert+c \\ &=\frac12\ln\left\vert\frac{1+2\sin\frac{x}2\cos\frac{x}2}{1-2\sin\frac{x}2\cos\frac{x}2}\right\vert+c \\ &=\frac12\ln\left\vert\frac{\cos^2\frac{x}2+\sin^2\frac{x}2+2\sin\frac{x}2\cos\frac{x}2}{\cos^2\frac{x}2+\sin^2\frac{x}2-2\sin\frac{x}2\cos\frac{x}2}\right\vert+c \\ &=\frac12\ln\left\vert\frac{\left(\cos\frac{x}2-\sin\frac{x}2\right)^2}{\left(\cos\frac{x}2+\sin\frac{x}2\right)^2}\right\vert+c \\ &=\ln\left\vert\frac{\cos\frac{x}2-\sin\frac{x}2}{\cos\frac{x}2+\sin\frac{x}2}\right\vert+c \\ &=\ln\left\vert\frac{1+\frac{\sin\frac{x}2}{\cos\frac{x}2}}{1-\frac{\sin\frac{x}2}{\cos\frac{x}2}}\right\vert+c \\ &=\ln\left\vert\frac{1+\tan\frac{x}2}{1-\tan\frac{x}2}\right\vert+c \qquad \square \end{align} $$
Check 2: 나아가 앞서 방법1에서 도출한 결과와 동일함도 확인할 수 있다.
$$ \begin{align} I&=\ln\left\vert\frac{1+\tan\frac{x}2}{1-\tan\frac{x}2}\right\vert+c \\ &=\ln\left\vert\frac{1+\frac{\sin\frac{x}2}{\cos\frac{x}2}}{1-\frac{\sin\frac{x}2}{\cos\frac{x}2}}\right\vert+c \\ &=\ln\left\vert\frac{\cos\frac{x}2+\sin\frac{x}2}{\cos\frac{x}2-\sin\frac{x}2}\right\vert+c \\ &=\ln\left\vert\frac{\cos\frac{x}2+\sin\frac{x}2}{\cos\frac{x}2-\sin\frac{x}2}\cdot\frac{\cos\frac{x}2+\sin\frac{x}2}{\cos\frac{x}2+\sin\frac{x}2}\right\vert+c \\ &=\ln\left\vert\frac{\left(\cos\frac{x}2+\sin\frac{x}2\right)^2}{\cos^2\frac{x}2-\sin^2\frac{x}2}\right\vert+c \\ &=\ln\left\vert\frac{\overbrace{\cos^2\frac{x}2+\sin^2\frac{x}2}^{=1}+\overbrace{2\sin\frac{x}2\cos\frac{x}2}^{=\sin x}}{\cos x}\right\vert+c \\ &=\ln\left\vert\frac{1+\sin x}{\cos x}\right\vert+c \\ &=\ln\vert\sec x+\tan x\vert+c \qquad \square \end{align} $$
4. 가장 오래된 결과
$$ \int\sec x\,\textrm{d}x=\ln\left\vert\tan\left(\frac{x}2+\frac{\pi}4\right)\right\vert+c $$
앞서 역사적 배경에서 설명한 것처럼 위 결과가 시컨트/세컨트 적분에 있어 가장 처음 알려진 결과다.
(1) 유도1: 이 결과는 다음과 같이 유도할 수 있다.
$$ \begin{align} \sec x&=\frac1{\cos x} \\ &=\frac1{\sin\left(x+\frac{\pi}2\right)} \\ &=\frac1{2\sin\left(\frac{x}2+\frac{\pi}4\right)\cos\left(\frac{x}2+\frac{\pi}4\right)} \\ &=\frac1{2\tan\left(\frac{x}2+\frac{\pi}4\right)\cos^2\left(\frac{x}2+\frac{\pi}4\right)} \\ &=\frac{\sec^2\left(\frac{x}2+\frac{\pi}4\right)}{2\tan\left(\frac{x}2+\frac{\pi}4\right)} \\ \Rightarrow\quad \int\sec x\,\textrm{d}x&=\int\frac{\frac12\sec^2\left(\frac{x}2+\frac{\pi}4\right)}{\tan\left(\frac{x}2+\frac{\pi}4\right)}\,\textrm{d}x=\ln\left\vert\tan\left(\frac{x}2+\frac{\pi}4\right)\right\vert+c \qquad \square \end{align}$$
(2) 유도2: $\tan\frac{\pi}4=1\,$과 $\tan(A+B)=\frac{\tan A+\tan B}{1-\tan A\tan B}\,$를 이용하여 방법3에서도 유도 가능하다.
$$ \begin{align} I&=\ln\left\vert\frac{1+\tan\frac{x}2}{1-\tan\frac{x}2}\right\vert+c \\ &=\ln\underbrace{\left\vert\frac{\tan\frac{\pi}4+\tan\frac{x}2}{1-\tan\frac{\pi}4\tan\frac{x}2}\right\vert}+c \\ &=\ln\left\vert\tan\left(\frac{x}2+\frac{\pi}4\right)\right\vert+c \qquad \square \end{align} $$
(3) 유도3: 방법3에서 소개된 t-치환의 변형된 꼴로도 유도 가능하다.
$$ \begin{align} && t&=\tan\left(\frac{x}2+\frac{\pi}4\right) \\ &\Rightarrow& \textrm{d}t&=\frac12\underbrace{\sec^2\left(\frac{x}2+\frac{\pi}4\right)}_{1+\tan^2\left(\frac{x}2+\frac{\pi}4\right)}\,\textrm{d}x=\frac{1+\tan^2\left(\frac{x}2+\frac{\pi}4\right)}2\,\textrm{d}x=\frac{1+t^2}2\,\textrm{d}x \\ &\Rightarrow& \textrm{d}x&=\frac{2}{1+t^2}\,\textrm{d}t \\ \\ && \cos x&=\sin\left(x+\frac{\pi}2\right)=2\sin\left(\frac{x}2+\frac{\pi}4\right)\cos\left(\frac{x}2+\frac{\pi}4\right)=2\cos^2\left(\frac{x}2+\frac{\pi}4\right)\tan\left(\frac{x}2+\frac{\pi}4\right) \\ &&&=\frac{2\tan\left(\frac{\pi}2+\frac{\pi}4\right)}{\sec^2\left(\frac{x}2+\frac{\pi}4\right)}=\frac{2\tan\left(\frac{x}2+\frac{\pi}4\right)}{1+\tan^2\left(\frac{x}2+\frac{\pi}4\right)}=\frac{2t}{1+t^2} \\ && \sin x&=\cos\left(x+\frac{\pi}2\right)=\cos^2\left(\frac{x}2+\frac{\pi}4\right)-\sin^2\left(\frac{x}2+\frac{\pi}4\right)=\cos^2\left(\frac{x}2+\frac{\pi}4\right)\left[1-\tan^2\left(\frac{x}2+\frac{\pi}4\right)\right] \\ &&&=\frac{1-\tan^2\left(\frac{x}2+\frac{\pi}4\right)}{\sec^2\left(\frac{x}2+\frac{\pi}4\right)}=\frac{1-\tan^2\left(\frac{x}2+\frac{\pi}4\right)}{1+\tan^2\left(\frac{x}2+\frac{\pi}4\right)}=\frac{1-t^2}{1+t^2} \end{align} $$
이 결과를 시컨트 적분에 적용하면,
$$ \begin{align} I&=\int\sec x\,\textrm{d}x \\ &=\int\frac1{\cos x}\, \textrm{d}x \\ &=\int\frac1{\frac{2t}{1+t^2}}\frac2{1+t^2}\,\textrm{d}t \\ &=\int\frac1t\,\textrm{d}t \\ &=\ln\vert t\vert+c \\ &=\ln\left\vert\tan\left(\frac{x}2+\frac{\pi}4\right)\right\vert+c \qquad \square \end{align} $$
5. 부록: t-치환 / 바이어슈트라스 치환 $t=\tan\frac{x}2$
t-치환으로 시컨트와 코시컨트 적분을 할 수 있지만, 이 두 적분만 하고 멈추기에 t-치환은 너무 효율적인 도구다.
앞서 유도한 결과를 다시 요약해보자.
$$ \textrm{d}x=\frac{2}{1+t^2}\,\textrm{d}t, \qquad \cos x=\frac{1-t^2}{1+t^2}, \qquad \sin x=\frac{2t}{1+t^2} $$
또한 다른 삼각함수($\tan$, $\sec$, $\csc$, $\cot$)도 t를 사용해 나타낼 수 있다.
$$ \tan x=\frac{2t}{1-t^2},\quad \sec x=\frac{1+t^2}{1-t^2}, \quad \csc x=\frac{1+t^2}{2t}, \quad \cot x=\frac{1-t^2}{2t} $$
이를 이용하면 $\cos x$, $\sin x$이 들어있는 모든 적분을 다음과 같이 쓸 수 있다.
$$ \int \textrm{f} (\cos x,\sin x)\,\textrm{d}x = \int \textrm{f} \left(\frac{1-t^2}{1+t^2},\frac{2t}{1+t^2}\right)\frac{2}{1+t^2}\,\textrm{d}t $$
이중 가장 대표적인 예는
$$\int\frac1{a\cos x+b\sin x+c}\,\textrm{d}x$$
로서 보다 자세한 내용은 t-치환/바이어슈트라스 치환(t-substitution, Weierstrass substitution)참조.
'수학 모음 (Maths collection) > Technical A - Exploring ideas' 카테고리의 다른 글
| 14. Integration of the square-root of tan x (0) | 2021.11.23 |
|---|---|
| 5. 쌍곡코시컨트(csch x)의 적분법 | Integration of csch x (0) | 2020.06.07 |
| 4. 쌍곡시컨트(sech x)의 적분법 | Integration of sech x (0) | 2020.06.07 |
| 3. 코시컨트/코세칸트(cosec x, csc x)의 적분법 | Integration of cosec x (0) | 2020.06.07 |
| 1. History of the Integral of the Secant (sec x) (0) | 2020.06.06 |


