| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 교육
- test
- factors
- 영국
- division
- triangle
- mathematics
- Oxford
- factor
- Partial
- solution
- 제도
- DENOMINATOR
- fractions
- Admissions
- Order
- algebraic
- a-level
- 학년
- College
- equation
- 바이어슈트라스
- Maths
- GCSE
- Weierstrass
- differential
- integral
- t-치환
- 치환
- 적분
- Today
- Total
목록수학 모음 (Maths collection)/Technical B - Problem solving (12)
Cambridge Maths Academy
수학 모음 (Maths collection) 전체보기 This question comes from a test paper for A-level maths for Michaelmas Term at Eton College. Q16. (a) Solve the equation $$ \begin{align} \log_{10}\left(3^x-5^{2-x}\right)=2+\log_{10}(2)-x\log_{10}(5), \end{align} $$ giving your answer as exact. [3 marks] (b) Solve the equation $$ \begin{align} \left(5\sqrt{5}\right)^{3x}-31=30\left(\frac1{\sqrt[4]{5}}\right)^{9x}, ..
수학 모음 (Maths collection) 전체보기 This question comes from a test paper for A-level maths for Michaelmas Term at Eton College. Q15. (a) Express $\cos(2\theta)+\sin(2\theta)$ in the form $R\sin(2\theta+\alpha)$ where $R>0$ and $0 < \alpha < \frac{\pi}{2}$. [3 marks] (b) Hence show that $$ \begin{align} \frac{1-\sqrt{2}}{2}\le \cos\theta(\cos\theta+\sin\theta) \le\frac{1+\sqrt{2}}{2} \end{align} $$ fo..
수학 모음 (Maths collection) 전체보기 This question comes from a test paper for A-level maths for Michaelmas Term at Eton College. Q14. At time $t$ secons after the start of an experiment, the temperature of a cooling liquid is proportional to $\textrm{e}^{-kt}$. (a) Given that the liquid's initial temperature was $80^\circ$C, find a formula for $T$ in terms of $t$ and $k$. [1 mark] (b) Given also that ..
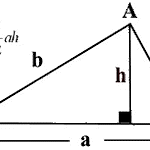 1. 헤론의 공식 유도 (A derivation of Heron's formula)
1. 헤론의 공식 유도 (A derivation of Heron's formula)
헤론의 공식(Heron's formula)은 삼각형의 넓이를 구하는 식이다. 여기서 우리는 삼각형의 넓이를 구하는 두 가지 버전의 공식을 살펴보고, 코사인 법칙(the cosine rule)을 사용하여 헤론의 공식을 유도해보자. $A=\frac12ah$ $A=\frac12ab\sin C$ 헤론의 공식: $A=\sqrt{s(s-a)(s-b)(s-c)}\,$, 그리고 $s=\frac{a+b+c}{2}\,$는 삼각형 둘레의 절반이다. 곧 살펴보겠지만 이 세 가지 공식은 하나의 공식에서 다른 공식을 유도할 수 있는 만큼 모두 동등하다. 따라서 문제에서 주어진 조건에 따라 이 세 가지 공식 중 적절한 것을 선택하여 사용하면 된다. 삼각형의 넓이 1 우리가 가장 먼저 배우는 삼각형의 넓이 공식은 다음과 같다. $$..
