| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 바이어슈트라스
- solution
- Order
- 교육
- 제도
- fractions
- 학년
- integral
- division
- 적분
- equation
- mathematics
- factors
- Admissions
- College
- 치환
- Weierstrass
- Oxford
- triangle
- t-치환
- Partial
- 영국
- factor
- test
- a-level
- GCSE
- DENOMINATOR
- differential
- Maths
- algebraic
- Today
- Total
Cambridge Maths Academy
1. 헤론의 공식 유도 (A derivation of Heron's formula) 본문
1. 헤론의 공식 유도 (A derivation of Heron's formula)
Cambridge Maths Academy 2020. 6. 22. 20:51
헤론의 공식(Heron's formula)은 삼각형의 넓이를 구하는 식이다. 여기서 우리는 삼각형의 넓이를 구하는 두 가지 버전의 공식을 살펴보고, 코사인 법칙(the cosine rule)을 사용하여 헤론의 공식을 유도해보자.
- $A=\frac12ah$
- $A=\frac12ab\sin C$
- 헤론의 공식: $A=\sqrt{s(s-a)(s-b)(s-c)}\,$, 그리고 $s=\frac{a+b+c}{2}\,$는 삼각형 둘레의 절반이다.
곧 살펴보겠지만 이 세 가지 공식은 하나의 공식에서 다른 공식을 유도할 수 있는 만큼 모두 동등하다. 따라서 문제에서 주어진 조건에 따라 이 세 가지 공식 중 적절한 것을 선택하여 사용하면 된다.
삼각형의 넓이 1
우리가 가장 먼저 배우는 삼각형의 넓이 공식은 다음과 같다.
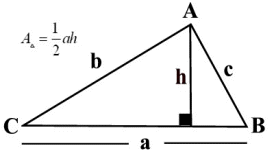
$$ {\rm Area}=\frac12\times{\rm 밑변}\times{\rm 높이}=\frac12ah$$
삼각형의 넓이 2: 삼각함수
위 공식에서 삼각함수를 이용하여 높이 h를 b와 각도 C로 나타낼 수 있다. 즉, $h=b\sin C$.
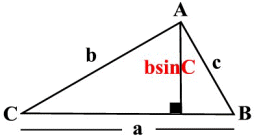
$$ A=\frac12ah=\frac12ab\sin C$$
Comment: 이 두 번째 공식은 두 변과 그 사잇각을 알 때 사용할 수 있는 공식이다.
코사인 법칙(The cosine rule)
헤론의 공식을 유도하기 위해서는 코사인 법칙을 알아야 한다. 코사인 법칙은 왼쪽 컬럼과 같이 세 가지 버전으로 나타낼 수 있는데, 세 변 중 무엇을 구하고자 하는가에 따라 세 가지로 표현한 것이다. 오른쪽 컬럼은 왼쪽의 공식에서 각도를 구할 수 있게끔 정리한 것이다.
$$ \begin{align} a^2&=b^2+c^2-2bc\cos A &&\Leftrightarrow& \cos A&=\frac{b^2+c^2-a^2}{2bc} \\ b^2&=c^2+a^2-2ca\cos B &&\Leftrightarrow& \cos B&=\frac{c^2+a^2-b^2}{2ca} \\ c^2&=a^2+b^2-2ab\cos C &&\Leftrightarrow& \cos C&=\frac{a^2+b^2-c^2}{2ab} \end{align} $$
- 왼쪽 컬럼을 보면 '삼각형의 세 번째 변의 길이는 나머지 두 변의 길이와 사잇각을 통해 구할 수 있다'.
- 오른쪽 컬럼을 보면 '삼각형의 세 각도는 세 변의 길이를 통해 구할 수 있다'.
Proof. 코사인 법칙은 피타고라스의 정리를 통해 증명 가능하다.
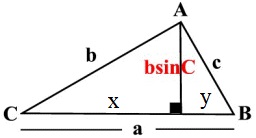
위 그림을 보면 왼쪽과 오른쪽, 두 개의 직각삼각형이 보인다. 여기서 왼쪽 직각삼각형의 밑변을 x, 오른쪽 직각삼각형의 밑변을 y라고 하자. 이 두 직각삼각형에 피타고라스의 정리를 적용하면 다음과 같다.
$$ \begin{align} {\rm 왼쪽\;삼각형}:\qquad x^2+h^2&=b^2 \\ {\rm 오른쪽\;삼각형}:\qquad y^2+h^2&=c^2 \\ \Rightarrow\qquad y^2-x^2&=c^2-b^2 \end{align} $$
이제 $y=a-x$ 와 $x=b\cos C$ 를 사용하면, $$ \begin{align} c^2&=b^2+y^2-x^2 \\ &=b^2+(a-x)^2-x^2 \\ &=b^2+a^2-2ax+x^2-x^2 \\ &=a^2+b^2-2ab\cos C\qquad\square \end{align} $$
삼각형의 넓이 3: 헤론의 공식(Heron's formula)
$$ A=\sqrt{s(s-a)(s-b)(s-c)},\qquad s=\frac{a+b+c}2 $$
이제 위에서 소개한 '삼각형의 넓이 2'에 해당하는 공식과 코사인 법칙(the cosine rule)을 이용하여 헤론의 공식을 유도할 수 있다.
$$ \begin{align} A&=\frac12ab\sin C \\ &=\frac12ab\sqrt{1-\cos^2C}\quad{\rm since}\quad \cos^2C+\sin^2C=1 \\ &=\frac12ab\sqrt{1-\left(\frac{a^2+b^2-c^2}{2ab}\right)^2} \\ &=\frac12ab\sqrt{1-\frac{\left(a^2+b^2-c^2\right)^2}{4a^2b^2}} \\ &=\frac14\sqrt{(2ab)^2-\left(a^2+b^2-c^2\right)^2} \\ &=\frac14\sqrt{\left(2ab+a^2+b^2-c^2\right)\left(2ab-a^2-b^2+c^2\right)} \\ &=\frac14\sqrt{\left[(a+b)^2-c^2\right]\left[c^2-(a-b)^2\right]} \\ &=\frac14\sqrt{(a+b+c)(a+b-c)(c+a-b)(c-a+b)} \\ &=\sqrt{\left(\frac{a+b+c}2\right)\left(\frac{a+b-c}2\right)\left(\frac{c+a-b}2\right)\left(\frac{c-a+b}2\right)} \\ &=\sqrt{\left(\frac{a+b+c}2\right)\left(\frac{a+b+c-2c}2\right)\left(\frac{c+a+b-2b}2\right)\left(\frac{c+a+b-2a}2\right)} \\ &=\sqrt{\left(\frac{a+b+c}2\right)\left(\frac{a+b+c}2-c\right)\left(\frac{c+a+b}2-b\right)\left(\frac{c+a+b}2-a\right)} \\ &=\sqrt{s(s-a)(s-b)(s-c)} \qquad\square \end{align}$$
Comment: 헤론의 공식은 세 변의 길이를 알 때 삼각형의 넓이를 구할 수 있는 식이다. 만약 헤론의 공식이 복잡하게 느껴진다면 굳이 외우고자 노력하지 않아도 된다. 왜냐하면 유도하는 과정에서 알 수 있듯이, 세 변을 알 때 코사인 법칙을 이용하여 세 각도 중 하나를 구할 수 있고, 그런 다음 '삼각형의 넓이 2' 공식을 사용하여 얼마든지 삼각형의 넓이를 구할 수 있기 때문이다. 즉, 헤론의 공식은 이 두 가지 과정을 한 번에 지나갈 수 있는 지름길로 봐도 무방하다.
Heron's formula calculates the area of a triangle. Here, we will look at two different formulae describing the area of a triangle and then derive the third version, Heron's formula.
- $A=\frac12ah$
- $A=\frac12ab\sin C$
- Heron's formula: $A=\sqrt{s(s-a)(s-b)(s-c)}\,$ where $s=\frac{a+b+c}{2}$. s can be thought of as half the perimeter of the triangle.
As we will see, they are all equivalent and therefore can be used interchangeably depending on the available conditions.
Area of a triangle 1
As widely known, the area of a triangle is:

$$ {\rm Area}=\frac12\times{\rm base}\times{\rm height}=\frac12ah$$
Area of a triangle 2: Trigonometry
We can express the height h in terms of b and the angle C using trigonometry, i.e. $h=b\sin C$
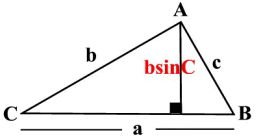
$$ A=\frac12ah=\frac12ab\sin C$$
Comment: This formula can be used when two sides and the angle between them are known.
The cosine rule
In order to derive Heron's formula, we need to recall what's commonly called the cosine rule:
$$ \begin{align} a^2&=b^2+c^2-2bc\cos A &&\Leftrightarrow& \cos A&=\frac{b^2+c^2-a^2}{2bc} \\ b^2&=c^2+a^2-2ca\cos B &&\Leftrightarrow& \cos B&=\frac{c^2+a^2-b^2}{2ca} \\ c^2&=a^2+b^2-2ab\cos C &&\Leftrightarrow& \cos C&=\frac{a^2+b^2-c^2}{2ab} \end{align} $$
- The left hand column says 'a length of a triangle can be expressed in terms of the other two lengths and the angle betweem them'.
- The right hand column says 'each angle can be expressed in terms of three lengths'.
Proof. The cosine rule can be proved by Pythagoras' theorem.
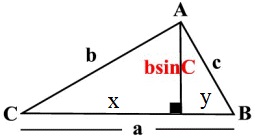
There are two right-angled triangles in the diagram such that their bases are x and y respectively. Pythagoras' theorem applied to them yield:
$$ \begin{align} {\rm Left-hand\;\triangle}:\qquad x^2+h^2&=b^2 \\ {\rm Right-hand\;\triangle}:\qquad y^2+h^2&=c^2 \\ \Rightarrow\qquad y^2-x^2&=c^2-b^2 \end{align} $$
Note that $y=a-x$ and $x=b\cos C$, $$ \begin{align} c^2&=b^2+y^2-x^2 \\ &=b^2+(a-x)^2-x^2 \\ &=b^2+a^2-2ax+x^2-x^2 \\ &=a^2+b^2-2ab\cos C\qquad\square \end{align} $$
Area of a triangle 3: Heron's formula
$$ A=\sqrt{s(s-a)(s-b)(s-c)},\qquad s=\frac{a+b+c}2 $$
Using the cosine rule, we can derive Heron's formula from the second version of the area of a triangle:
$$ \begin{align} A&=\frac12ab\sin C \\ &=\frac12ab\sqrt{1-\cos^2C}\quad{\rm since}\quad \cos^2C+\sin^2C=1 \\ &=\frac12ab\sqrt{1-\left(\frac{a^2+b^2-c^2}{2ab}\right)^2} \\ &=\frac12ab\sqrt{1-\frac{\left(a^2+b^2-c^2\right)^2}{4a^2b^2}} \\ &=\frac14\sqrt{(2ab)^2-\left(a^2+b^2-c^2\right)^2} \\ &=\frac14\sqrt{\left(2ab+a^2+b^2-c^2\right)\left(2ab-a^2-b^2+c^2\right)} \\ &=\frac14\sqrt{\left[(a+b)^2-c^2\right]\left[c^2-(a-b)^2\right]} \\ &=\frac14\sqrt{(a+b+c)(a+b-c)(c+a-b)(c-a+b)} \\ &=\sqrt{\left(\frac{a+b+c}2\right)\left(\frac{a+b-c}2\right)\left(\frac{c+a-b}2\right)\left(\frac{c-a+b}2\right)} \\ &=\sqrt{\left(\frac{a+b+c}2\right)\left(\frac{a+b+c-2c}2\right)\left(\frac{c+a+b-2b}2\right)\left(\frac{c+a+b-2a}2\right)} \\ &=\sqrt{\left(\frac{a+b+c}2\right)\left(\frac{a+b+c}2-c\right)\left(\frac{c+a+b}2-b\right)\left(\frac{c+a+b}2-a\right)} \\ &=\sqrt{s(s-a)(s-b)(s-c)} \qquad\square \end{align}$$
Comment: Heron's formula can be used when three sides (and no angles) of a triangle are known. To remind you, while this is a convenient formula as long as one remembers its form, one can always work out one of the angles using the cosine rule and then use $\frac12ab\sin C$. Heron's formula only provides a short-cut.
'수학 모음 (Maths collection) > Technical B - Problem solving' 카테고리의 다른 글
| 6. Probability - Jumping goldfish (GCSE) (0) | 2020.12.29 |
|---|---|
| 5. A counting problem - Lucy & Anton in the photo (GCSE) (0) | 2020.12.29 |
| 4. A question on logarithms (Eton College 01C_MT1 Q16) (0) | 2020.12.09 |
| 3. A question on trigonometry (Eton College 01C_MT1 Q15) (0) | 2020.12.09 |
| 2. A question on exponential decay (Eton College 01C_MT1 Q14) (0) | 2020.12.09 |
