| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 영국
- equation
- integral
- 교육
- 학년
- 적분
- DENOMINATOR
- College
- fractions
- differential
- Weierstrass
- test
- Oxford
- factors
- Partial
- GCSE
- t-치환
- algebraic
- a-level
- triangle
- Admissions
- Maths
- Order
- division
- factor
- 치환
- solution
- 바이어슈트라스
- mathematics
- 제도
- Today
- Total
목록rule (2)
Cambridge Maths Academy
수학 모음 (Maths collection) 전체보기 Question. Find $\frac{dy}{dx}$ for: $$ \begin{align} \textrm{(a)}&\qquad y = \arcsin(1-2x) \\ \textrm{(b)}&\qquad y = \arctan\left(x^2+1\right) \end{align} $$ Solution. (a) For $y=\arcsin(1-2x)$, we have $$ \begin{gather} -1\le 1-2x \le 1 \\ -\frac{\pi}{2}\le y \le\frac{\pi}{2} \end{gather} $$ We re-express the equation $$ \begin{align} y&=\arcsin(1-2x) \\ \Rightarr..
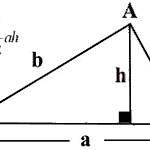 8. Heron's formula - Derivation
8. Heron's formula - Derivation
수학 모음 (Maths collection) 전체보기 Heron's formula calculates the area of a triangle. Here, we will look at two different formulae describing the area of a triangle and then derive the third version, Heron's formula. $A=\frac12ah$ $A=\frac12ab\sin C$ Heron's formula: $A=\sqrt{s(s-a)(s-b)(s-c)}\,$ where $s=\frac{a+b+c}{2}$. s can be thought of as half the perimeter of the triangle. As we will see, the..
