| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- integral
- Oxford
- Weierstrass
- Partial
- equation
- triangle
- mathematics
- t-치환
- Maths
- 적분
- test
- 바이어슈트라스
- Admissions
- solution
- College
- 영국
- Order
- 치환
- fractions
- 학년
- 제도
- factors
- division
- differential
- algebraic
- 교육
- DENOMINATOR
- GCSE
- a-level
- factor
- Today
- Total
목록quadratic (2)
Cambridge Maths Academy
Pure mathematics Year 2 Table of contents Partial fractions revisited Partial fractions with repeated factors Examples Edexcel P2 Ch1 Exercise 1E The main task of this section is to understand partial fractions with repeated factors. In order to do so, we need to consider and understand some general form of fractions. 1. Partial fractions revisited In the previous section, P2 §1.3 Partial fracti..
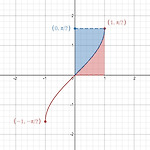 8. Some integrals
8. Some integrals
수학 모음 (Maths collection) 전체보기 Question. Evaluate the following integrals: $$ \begin{align} {\rm (a)}&& &\int\frac{1}{\sqrt{1-3x^2}}\,\textrm{d}x \\ {\rm (b)}&& &\int\frac{x}{4x^2+8x+13}\,\textrm{d}x \\ {\rm (c)}&& &\int_0^1\arcsin x\,\textrm{d}x \end{align} $$ Solution. (a) By substitution, $$ \begin{align} x&=\frac1{\sqrt{3}}\sin u \\ \Rightarrow\quad \textrm{d}x&=\frac1{\sqrt{3}}\cos u\,\textr..
