| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- factor
- Admissions
- 교육
- Partial
- a-level
- test
- differential
- factors
- 적분
- 학년
- solution
- equation
- Order
- 치환
- 바이어슈트라스
- Oxford
- integral
- 영국
- division
- algebraic
- Weierstrass
- DENOMINATOR
- 제도
- fractions
- mathematics
- triangle
- t-치환
- GCSE
- College
- Maths
- Today
- Total
목록넓이 (2)
Cambridge Maths Academy
 19. 원뿔의 표면적 구하기
19. 원뿔의 표면적 구하기
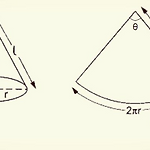
원뿔의 표면적을 구하기 위해서 전개도를 고려한다. 전개도는 원뿔을 잘라 펼친 그림의 의미한다. 전개도에서 부채꼴(sector)의 넓이와 원의 넓이를 구한 다음 둘의 넓이를 더하면 된다. 부채꼴의 넓이: 부채꼴 안에 있는 각도 $\theta$를 구해야 하는데, 이는 호의 길이를 고려하여 구할 수 있다. $$ \begin{align} L=2\pi\ell\times\frac{\theta}{360}&=2\pi r \\ \Rightarrow\quad \ell\times\frac{\theta}{360}&=r \end{align} $$ 부채꼴(sector)의 넓이: $$ \begin{align} A_{\rm sector}&=\pi\ell^2\times\frac{\theta}{360} \\ &=\pi\ell\times..
 1. 헤론의 공식 유도 (A derivation of Heron's formula)
1. 헤론의 공식 유도 (A derivation of Heron's formula)
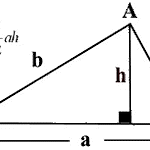
헤론의 공식(Heron's formula)은 삼각형의 넓이를 구하는 식이다. 여기서 우리는 삼각형의 넓이를 구하는 두 가지 버전의 공식을 살펴보고, 코사인 법칙(the cosine rule)을 사용하여 헤론의 공식을 유도해보자. $A=\frac12ah$ $A=\frac12ab\sin C$ 헤론의 공식: $A=\sqrt{s(s-a)(s-b)(s-c)}\,$, 그리고 $s=\frac{a+b+c}{2}\,$는 삼각형 둘레의 절반이다. 곧 살펴보겠지만 이 세 가지 공식은 하나의 공식에서 다른 공식을 유도할 수 있는 만큼 모두 동등하다. 따라서 문제에서 주어진 조건에 따라 이 세 가지 공식 중 적절한 것을 선택하여 사용하면 된다. 삼각형의 넓이 1 우리가 가장 먼저 배우는 삼각형의 넓이 공식은 다음과 같다. $$..
