| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- Maths
- solution
- Admissions
- test
- DENOMINATOR
- Order
- 적분
- fractions
- a-level
- triangle
- Oxford
- 영국
- mathematics
- 바이어슈트라스
- GCSE
- factors
- 학년
- Weierstrass
- 교육
- factor
- Partial
- differential
- equation
- 제도
- College
- t-치환
- 치환
- division
- algebraic
- integral
- Today
- Total
목록Log (3)
Cambridge Maths Academy
수학 모음 (Maths collection) 전체보기 This post has been partly motivated by P2 §11.6 Integration by parts CP2 §6.5 Integrating hyperbolic functions CP2 §7.1 First-order differential equations (obtaining the particular integrals using the integrating factor) Question. Derive the following results. $$ \begin{align} \textrm{(a)} &&& I_1(a,b) = \int \textrm e^{ ax } \cos b x \, \textrm dx = \frac{ \textrm ..
We have: $$ \begin{align} 1^1&=1 &&& 0^1&=0 \\ 1^0&=1 &&& 0^0&=1 \end{align} $$ Are you surprised by $0^0=1$? Proof. To prove this, we consider $$ \begin{align} y=x^x \end{align} $$ and take the limit $x\rightarrow0$. It is not straightforward to do this directly with $x^x$ so we take the (natural or any) logarithm on both sides: $$ \begin{align} \ln y=\ln x^x=x\ln x \end{align} $$ Let $x=e^{-n}..
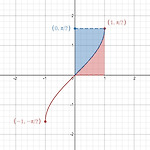 8. Some integrals
8. Some integrals
수학 모음 (Maths collection) 전체보기 Question. Evaluate the following integrals: $$ \begin{align} {\rm (a)}&& &\int\frac{1}{\sqrt{1-3x^2}}\,\textrm{d}x \\ {\rm (b)}&& &\int\frac{x}{4x^2+8x+13}\,\textrm{d}x \\ {\rm (c)}&& &\int_0^1\arcsin x\,\textrm{d}x \end{align} $$ Solution. (a) By substitution, $$ \begin{align} x&=\frac1{\sqrt{3}}\sin u \\ \Rightarrow\quad \textrm{d}x&=\frac1{\sqrt{3}}\cos u\,\textr..
