| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- triangle
- DENOMINATOR
- integral
- 영국
- equation
- GCSE
- 교육
- Partial
- 적분
- factors
- differential
- Oxford
- 제도
- test
- fractions
- mathematics
- t-치환
- factor
- Maths
- 치환
- Admissions
- a-level
- College
- Order
- 학년
- Weierstrass
- 바이어슈트라스
- solution
- algebraic
- division
Archives
- Today
- Total
목록원뿔 (1)
Cambridge Maths Academy
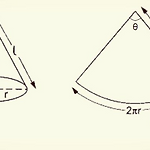 19. 원뿔의 표면적 구하기
19. 원뿔의 표면적 구하기
원뿔의 표면적을 구하기 위해서 전개도를 고려한다. 전개도는 원뿔을 잘라 펼친 그림의 의미한다. 전개도에서 부채꼴(sector)의 넓이와 원의 넓이를 구한 다음 둘의 넓이를 더하면 된다. 부채꼴의 넓이: 부채꼴 안에 있는 각도 $\theta$를 구해야 하는데, 이는 호의 길이를 고려하여 구할 수 있다. $$ \begin{align} L=2\pi\ell\times\frac{\theta}{360}&=2\pi r \\ \Rightarrow\quad \ell\times\frac{\theta}{360}&=r \end{align} $$ 부채꼴(sector)의 넓이: $$ \begin{align} A_{\rm sector}&=\pi\ell^2\times\frac{\theta}{360} \\ &=\pi\ell\times..
물리 모음 (Physics collection)
2021. 1. 14. 09:08
