| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- Maths
- Admissions
- Order
- equation
- 적분
- 제도
- 영국
- factors
- integral
- algebraic
- DENOMINATOR
- test
- 교육
- a-level
- solution
- mathematics
- fractions
- t-치환
- triangle
- differential
- Oxford
- 바이어슈트라스
- 치환
- factor
- College
- division
- 학년
- Partial
- GCSE
- Weierstrass
- Today
- Total
목록substitution (2)
Cambridge Maths Academy
Pure mathematics Year 2 Table of contents Partial fractions Examples Edexcel P2 Ch1 Exercise 1D 1. Partial fractions In the previous section, P2 §1.2 Algebraic fractions, we learnt how to add and subtract two (or more) fractions, e.g. $$ \frac{2}{x+3} - \frac{1}{x+1} = \frac{x-1}{(x+3)(x+1)} $$ Now, we can perform the reverse. In other words, a single fraction with two distinct linear factors in..
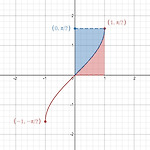 8. Some integrals
8. Some integrals
수학 모음 (Maths collection) 전체보기 Question. Evaluate the following integrals: $$ \begin{align} {\rm (a)}&& &\int\frac{1}{\sqrt{1-3x^2}}\,\textrm{d}x \\ {\rm (b)}&& &\int\frac{x}{4x^2+8x+13}\,\textrm{d}x \\ {\rm (c)}&& &\int_0^1\arcsin x\,\textrm{d}x \end{align} $$ Solution. (a) By substitution, $$ \begin{align} x&=\frac1{\sqrt{3}}\sin u \\ \Rightarrow\quad \textrm{d}x&=\frac1{\sqrt{3}}\cos u\,\textr..
