| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- GCSE
- 교육
- mathematics
- 학년
- Partial
- 치환
- Admissions
- differential
- fractions
- Maths
- DENOMINATOR
- Oxford
- 영국
- t-치환
- 제도
- a-level
- factors
- equation
- solution
- triangle
- College
- algebraic
- 바이어슈트라스
- 적분
- integral
- Weierstrass
- division
- factor
- test
- Order
- Today
- Total
Cambridge Maths Academy
CP2 §7.1 First-order differential equations 본문
CP2 §7.1 First-order differential equations
Cambridge Maths Academy 2020. 12. 21. 04:16
Core pure mathematics 2
Table of contents
- First example - the method of separable variables
- Removing the modulus sign
- First-order DEs with the method of the integrating factor (I.F.)
- Second example
- Two important questions for the integrating factor
- More examples
- Exercise 7A
- First-order differential equations with constant coefficients
1. First example - the method of separable variables
If a first-order differential equation can be written in the form $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } = \textrm f(x) \textrm g(y) \end{align} $$ then we can separate the variables: $$ \begin{align} \frac1{g(y)} \frac{ \textrm{d}y }{ \textrm{d}x } = \textrm f(x) \end{align} $$ and solve it by integrating both sides: $$ \begin{align} && \int \left( \frac1{g(y)} \frac{ \textrm{d}y }{ \textrm{d}x } \right) \, \textrm{d}x &= \int \textrm f(x) \, \textrm{d}x \\ & \Rightarrow & \int \frac1{g(y)} \, \textrm{d}y &= \int \textrm f(x) \, \textrm{d}x \end{align} $$ The process of separating the variables was briefly mentioned in P2 §11.10 Solving differential equations.
Example 1. Find the general solution to the differential equation $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } = - \frac{y}{x} \end{align} $$ and sketch members of the family of solution curves represented by the general solution.
Solution.
By the method of separable variables, $$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= - \frac{y}{x} \\ &\Rightarrow& \frac1{y}\frac{ \textrm{d}y }{ \textrm{d}x } &= -\frac1{x} \\ &\Rightarrow& \int \left( \frac1{y}\frac{ \textrm{d}y }{ \textrm{d}x } \right) \, \textrm{d}x &= - \int \frac1{x} \, \textrm{d}x \\ &\Rightarrow& \ln |y| &= - \ln |x| + \ln A = \ln \frac{A}{|x|} \\ &\Rightarrow& |y| &= \frac{A}{|x|} \qquad (\textrm{since} \; y=\ln x \; \textrm{is a 1-to-1 function}) \end{align} $$
We may remove the modulus sign by considering different possibilities:
(i) $x>0$, $y>0$ $$ \begin{align} y&= \frac{A}{x} \quad \textrm{with} \quad A>0 \end{align} $$ (ii) $x>0$, $y<0$ $$ \begin{align} y&= \frac{A}{x} \quad \textrm{with} \quad A<0 \end{align} $$ (iii) $x<0$, $y>0$ $$ \begin{align} y&= \frac{A}{x} \quad \textrm{with} \quad A<0 \end{align} $$ (iv) $x<0$, $y<0$ $$ \begin{align} y&= \frac{A}{x} \quad \textrm{with} \quad A>0 \end{align} $$ Thus, we find that, by allowing $A$ to be a real number, we may write the solution as: $$ \begin{align} y&= \frac{A}{x} \quad \textrm{where} \quad A \in \mathbb R \end{align} $$

Comment. Having gone through the four possibilities above, we may approach the result more directly using: $$ \begin{align} |x| = A \qquad \Rightarrow \qquad x = \pm A \end{align} $$ we find: $$ \begin{align} |y| = \frac{A}{|x|}, \quad A>0 \qquad \Rightarrow \qquad y = \pm \frac{A}{x}, \quad A>0 \end{align} $$ The only possible confusion with this expression is that the presence of $\pm$ does not mean that there are two solutions simultaneously unlike the modulus equations in general, i.e. the solution is either $y = A/x$ or $y = -A/x$. In order to remove this ambiguity, it is better to absorb the sign $\pm$ into A and write it as: $$ \begin{align} y = \frac{A}{x} \quad \textrm{where} \quad A \in \mathbb R \end{align} $$
2. Removing the modulus sign
When solving differential equations, the modulus signs crop up quite often due to the integral of the form $$ \begin{align} \int \frac1{ax+b} \, \textrm{d}x \end{align} $$ Let us consider a more general case: $$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= \frac{\textrm{g}(y)}{\textrm{g}'(y)} \frac{\textrm{f}'(x)}{\textrm{f}(x)} \\ &\Rightarrow& \frac{\textrm{g}'(y)}{\textrm{g}(y)}\frac{ \textrm{d}y }{ \textrm{d}x } &= \frac{\textrm{f}'(x)}{\textrm{f}(x)} \\ &\Rightarrow& \int \frac{\textrm{g}'(y)}{\textrm{g}(y)} \, \textrm{d}y &= \int \frac{\textrm{f}'(x)}{\textrm{f}(x)} \, \textrm{d}x \\ &\Rightarrow& \ln |\textrm{g}(y)| &= \ln |\textrm{f}(x)| + \ln A \\ &\Rightarrow& |\textrm{g}(y)| &= A|\textrm{f}(x)| \end{align} $$
There are four possibilities to consider:
(i) $\textrm{f}(x)>0$, $\textrm{g}(y)>0$ $$ \begin{align} \textrm{g}(y) = A \textrm{f}(x) \quad \textrm{with} \quad A>0 \end{align} $$ (ii) $\textrm{f}(x)>0$, $\textrm{g}(y)<0$ $$ \begin{align} \textrm{g}(y) = A \textrm{f}(x) \quad \textrm{with} \quad A<0 \end{align} $$ (iii) $\textrm{f}(x)<0$, $\textrm{g}(y)>0$ $$ \begin{align} \textrm{g}(y) = A \textrm{f}(x) \quad \textrm{with} \quad A<0 \end{align} $$ (iv) $\textrm{f}(x)<0$, $\textrm{g}(y)<0$ $$ \begin{align} \textrm{g}(y) = A \textrm{f}(x) \quad \textrm{with} \quad A>0 \end{align} $$ Thus, we find that, by allowing $A$ to be a real number, we may remove the modulus signs from both sides and write the solution as: $$ \begin{align} \textrm{g}(y) = A \textrm{f}(x) \quad \textrm{where} \quad A \in \mathbb R \end{align} $$
3. First-order DEs with the method of the integrating factor (I.F.)
A general first-order differential equation may be written as: $$ \begin{align} \textrm a(x,y) \frac{ \textrm{d}y }{ \textrm{d}x } + \textrm b(x,y) y = \textrm c(x,y) \end{align} $$ In this section, we learn a simpler version by remove the $y$-dependence of the coefficients: $$ \begin{align} && \textrm a(x) \frac{ \textrm{d}y }{ \textrm{d}x } + \textrm b(x) y &= \textrm c(x) \\ \\ &\Rightarrow & \frac{ \textrm{d}y }{ \textrm{d}x } + \underbrace{ \left[ \frac{ \textrm b(x) }{ \textrm a(x) } \right] }_{ \textrm{p}(x) } y &= \underbrace{ \left[ \frac{ \textrm c(x) }{ \textrm a(x) } \right] }_{ \textrm{q}(x) } \\ \\ &\Leftrightarrow & \frac{ \textrm{d}y }{ \textrm{d}x } + \textrm{p}(x) y &= \textrm{q}(x) \qquad (*) \end{align} $$
Still, this cannot be solved by separating variables. Instead, the produce rule 'in reverse' can be used to find a solution.
1) Step 1: Note that the product rule gives $$ \begin{align} \frac{ \textrm{d} }{ \textrm{d}x } \Big[ \textrm{f}(x) y \Big] = \textrm{f}(x) \frac{ \textrm{d}y }{ \textrm{d}x } + \textrm{f}'(x) y \end{align} $$ We notice that this also contains $\frac{ \textrm{d}y }{ \textrm{d}x }$ and $y$.
2) Step 2: Now, if we multiply the LHS of (*) by $\textrm{f}(x)$, it becomes to look like an exact derivative of a product as the RHS above, $$ \begin{align} \textrm{f}(x) \times (*) = \textrm{f}(x) \frac{ \textrm{d}y }{ \textrm{d}x } + \textrm{f}(x) \textrm{p}(x) y \end{align} $$
3) Step 3: If $\textrm f(x)$ satisfies $\textrm{f}(x) \textrm{p}(x) = \textrm{f}'(x)$, we'll have: $$ \begin{align} && \underbrace{ \textrm{f}(x) \frac{ \textrm{d}y }{ \textrm{d}x } + \textrm{f}(x) \textrm{p}(x) y }_{ \textrm{f}(x) \frac{ \textrm{d}y }{ \textrm{d}x } + \textrm{f}'(x) y } &= \textrm{f}(x) \textrm{q}(x) \\ \\ &\Rightarrow& \frac{ \textrm{d} }{ \textrm{d}x }\Big[ \textrm{f}(x) y \Big] &= \textrm{f}(x) \textrm{q}(x) \qquad (**) \end{align} $$
which can be integrated.
4) Step 4: Our final task is to find such $\textrm f(x)$ and this is called the integrating factor - a factor that enables integration. This is subject to the condition above, i.e. $\textrm{f}(x)$ is determined in terms of $\textrm{p}(x)$ as follows: $$ \begin{align} && \textrm{f}'(x) = \frac{ \textrm{d} \textrm f }{ \textrm{d}x } &= \textrm{f}(x) \textrm{p}(x) \\ &\Rightarrow& \frac1{ \textrm{f} }\frac{ \textrm{d} \textrm f }{ \textrm{d}x } &= \textrm p(x) \\ &\Rightarrow& \ln | \textrm{f}(x) | &= \int \textrm{p}(x) \, \textrm{d}x \\ \\ &\Rightarrow& \textrm{f}(x) &= \textrm{e}^{ \int \textrm{p}(x) \, \textrm{d}x } \end{align} $$
5) Aside. Finally, we may integrate (**) and find the general solution. The final form may appear rather complicated but, when it's applied to specific problems, it is not that bad so one does not need to remember this final result. $$ \begin{align} && \frac{ \textrm{d} }{ \textrm{d}x }\left[ \textrm{e}^{ \int \textrm{p}(x) \, \textrm{d}x } y \right] &= \textrm{e}^{ \int \textrm{p}(x) \, \textrm{d}x } \textrm{q}(x) \\ &\Rightarrow& \textrm{e}^{ \int \textrm{p}(x) \, \textrm{d}x } y &= \int \left[ \textrm{e}^{ \int \textrm{p}(x) \, \textrm{d}x } \textrm{q}(x) \right] \, \textrm{d}x \\ &\Rightarrow& y&= \textrm{e}^{ - \int \textrm{p}(x) \, \textrm{d}x } \int \left[ \textrm{e}^{ \int \textrm{p}(x) \, \textrm{d}x } \textrm{q}(x) \right] \, \textrm{d}x \end{align} $$
4. Second example
Example 2. Find the general solution to the differential equation $$ \begin{align} x^3 \frac{ \textrm{d}y }{ \textrm{d}x } + 3x^2 y = \sin x \end{align} $$
Solution 1. The LHS of the equation happens to be in a nice form: $$ \begin{align} && x^3 \frac{ \textrm{d}y }{ \textrm{d}x } + 3x^2 y = \frac{ \textrm{d} }{ \textrm{d}x } \left( x^3 y \right) &= \sin x \\ &\Rightarrow& x^3 y &= \int \sin x \, \textrm{d}x = - \cos x + C \\ \\ &\Rightarrow& y &= \frac{ - \cos x + C }{ x^3 } \end{align} $$
Solution 2. If we don't recognise the LHS, then we would start by dividing the equation by $x^3$. $$ \begin{align} x^3 \frac{ \textrm{d}y }{ \textrm{d}x } + 3x^2 y &= \sin x \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{3}{x} y &= \frac{ \sin x }{ x^3 } \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) &= \textrm{e}^{ \int \textrm p(x) \, \textrm{d}x } \\ &= \textrm{e}^{ \int \frac{3}{x} \, \textrm{d}x } \\ &= \textrm{e}^{ 3 \ln |x| } \\ &= \textrm{e}^{ \ln |x|^3 } \\ &= x^3 \end{align} $$ Multiplying the equation by $\textrm f(x)=x^3$ gives the original equation back which confirms that it was in the exact form: $$ \begin{align} && x^3 \frac{ \textrm{d}y }{ \textrm{d}x } + 3x^2 y = \frac{ \textrm{d} }{ \textrm{d}x } \left( x^3 y \right) &= \sin x \\ &\Rightarrow& x^3 y &= \int \sin x \, \textrm{d}x = - \cos x + C \\ \\ &\Rightarrow& y &= \frac{ - \cos x + C }{ x^3 } \end{align} $$
5. Two important questions for the integrating factor
Question 1. Where is the integation constant in the integrating factor?
In the example above, recall the integrating factor: $$ \begin{align} \textrm f(x) &= \textrm{e}^{ \int \frac{3}{x} \, \textrm{d}x } \\ &= \textrm{e}^{ \ln |x|^3 + C } \\ &= \textrm{e}^C \textrm{e}^{ \ln |x|^3 } \end{align} $$ So, in principle, we should multiply the equation by the expression above so let's proceed: $$ \begin{align} {\color{blue}{\textrm{e}^C}} \textrm{e}^{ \ln |x|^3 } \frac{ \textrm{d}y }{ \textrm{d}x } + {\color{blue}{\textrm{e}^C}} \textrm{e}^{ \ln |x|^3 } \frac3{x} y &= {\color{blue}{\textrm{e}^C}} \textrm{e}^{ \ln |x|^3 } \frac{ \sin x }{ x^3 } \end{align} $$ Now, we see that the factor $\textrm{e}^C$ can be cancalled on both sides so, from now on, we may ignore the integration constant for the integrating factor.
Question 2. How can we remove the modulus sign in the integrating factor?
The integrating factor now reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ \ln |x|^3 } = |x|^3 = \left\{ \begin{array}{lcl} x^3 & \textrm{for} & x\ge 0 \\ -x^3 & \textrm{for} & x < 0 \end{array} \right. \end{align} $$
However, as we multiply the differential equation by $\textrm f(x)$, the sign becomes insignificant as it can be cancelled on both sides, i.e.
(i) For $x \ge 0$, we have $\textrm f(x) = x^3$: $$ \begin{align} x^3 \frac{ \textrm{d}y }{ \textrm{d}x } + 3x^2 y = \sin x \end{align} $$ (ii) For $x < 0$, we have $\textrm f(x) = - x^3$: $$ \begin{align} - x^3 \frac{ \textrm{d}y }{ \textrm{d}x } - 3x^2 y = - \sin x \end{align} $$ and yet we arrive at the same equation. So, from now on, we may ignore the modulus sign in the integrating factor.
6. More examples
Example 3. Find the general solution of the differential equation $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } - 4y = \textrm{e}^x \end{align} $$
Solution. The integrating factor reads: $$ \begin{align} \textrm f(x) &= \textrm{e}^{ \int -4 \, \textrm{d}x } \\ &= \textrm{e}^{ -4x } \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & \textrm{e}^{ -4x } \frac{ \textrm{d}y }{ \textrm{d}x } - 4 \textrm{e}^{ -4x } y &= \textrm{e}^{ -4x } \textrm{e}^x \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ \textrm{e}^{ -4x } y \Big] &= \textrm{e}^{ -3x } \\ & \Rightarrow & \textrm{e}^{ -4x } y &= \int \textrm{e}^{ -3x } \, \textrm{d}x \\ &&&= -\frac13 \textrm{e}^{ -3x } + C \\ \\ & \Rightarrow & y &= -\frac13 \textrm{e}^x + C \textrm{e}^{4x} \end{align} $$
Comment 1. When solving a differential equation, we are essentially integrating the equation in the sense that $\frac{ \textrm{d}y }{ \textrm{d}x }$ and leave only $y$. Therefore, the final result contains the constant(s) of integration - also known as the arbitrary constant(s). For first-order differential equations, we get one integration constant. For second order DEs, we get two integration constants and so on. This final result with arbitrary constants is called the general solution.
Comment 2. In some questions, we will be given a boundary condition, such as $y=1$ when $x=0$. We can use this condition to find the value of the arbitrary constant, generating a particular solution. Different boundary conditions will give rise to different particular solutions.
Example 4. (a) Find the general solution of the differential equation $$ \begin{align} \cos x \frac{ \textrm{d}y }{ \textrm{d}x } + 2y \sin x = \cos^4 x \end{align} $$
(b) Find the particular solution which satisfies the condition that $y=2$ when $x=0$.
Solution. (a) We need to re-write the differential equation by dividing it by $\cos x$: $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{ 2 \sin x }{ \cos x } y = \cos^3 x \end{align} $$ The integrating factor reads: $$ \begin{align} \textrm f(x) &= \textrm{e}^{ \int \frac{ 2 \sin x }{ \cos x } \, \textrm{d}x } \\ &= \textrm{e}^{ - 2 \ln | \cos x | } \\ &= \textrm{e}^{ \ln | \sec x |^2 } \\ &= \sec^2x \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & \sec^2x \frac{ \textrm{d}y }{ \textrm{d}x } + \sec^2x \frac{ 2 \sin x }{ \cos x } y &= \sec^2x \cos^3x \\ & \Rightarrow & \frac1{ \cos^2x } \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{ 2 \sin x }{ \cos^3 x } y &= \cos x \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \left[ \frac{1}{ \cos^2x } y \right] &= \cos x \\ & \Rightarrow & \frac{1}{ \cos^2x } y &= \int \cos x \, \textrm{d}x \\ &&&= \sin x + C \\ \\ & \Rightarrow & y &= ( \sin x + C ) \cos^2x \end{align} $$
(b) We apply the boundary condition $(x,y)=(0,2)$:
$$ \begin{align} 2 &= ( \sin 0 + C ) \cos^20 \qquad \Rightarrow \qquad C = 2 \end{align} $$ so we find a particular solution subject to the given boundary condition: $$ \begin{align} y = ( \sin x + 2 ) \cos^2x \end{align} $$
Aside. In the diagram below, we see that the boundary condition $(0,2)$ singles out the particular solution among a family of solutions.
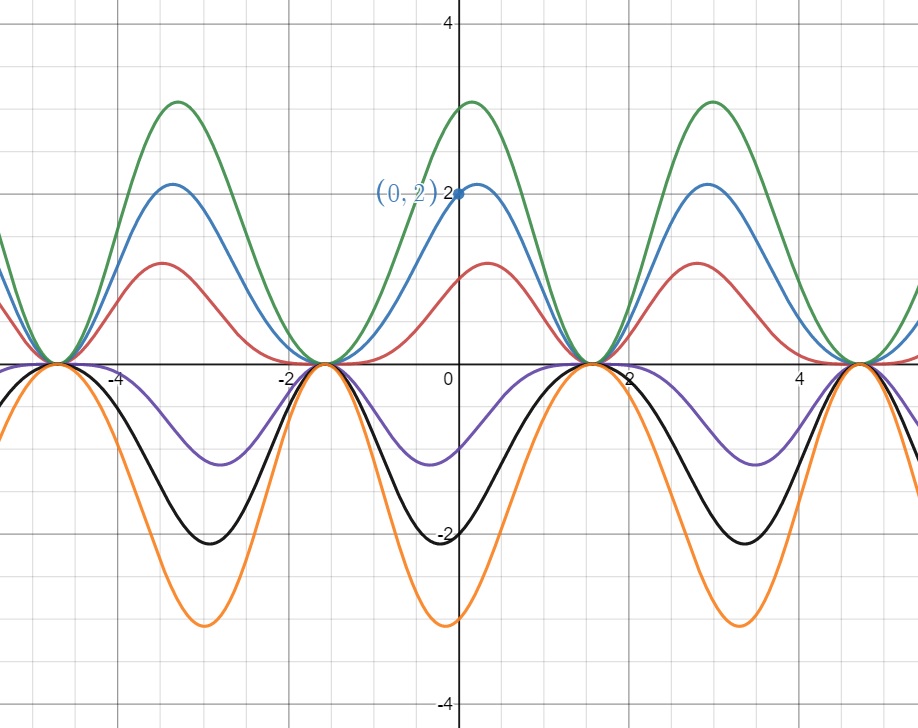
7. Exercise 7A
Question 1. For each of the following differential equations, find the general solution and sketch the family of solution curves. $$ \begin{align} \textbf{(a)}&& \frac{ \textrm{d}y }{ \textrm{d}x } &= 2x &&& \textbf{(b)}&& \frac{ \textrm{d}y }{ \textrm{d}x } &= y \\ \\ \textbf{(c)}&& \frac{ \textrm{d}y }{ \textrm{d}x } &= \frac{2y}{x} &&& \textbf{(d)}&& \frac{ \textrm{d}y }{ \textrm{d}x } &= \frac{x}{y} \\ \\ \textbf{(e)}&& \frac{ \textrm{d}y }{ \textrm{d}x } &= \cos x &&& \textbf{(f)}&& \frac{ \textrm{d}y }{ \textrm{d}x } &= y \cot x, \quad 0 < x < \pi \end{align} $$
Solution.
(a)
$$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= 2x \\ &\Rightarrow& y &= x^2 + C \end{align} $$
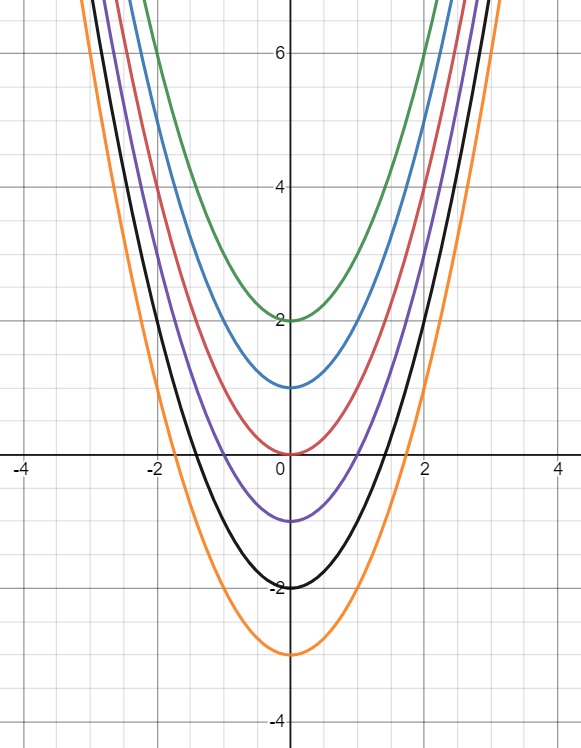
(b)
$$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= y \\ &\Rightarrow& \frac{1}{y}\frac{ \textrm{d}y }{ \textrm{d}x } &= 1 \\ &\Rightarrow& \int \frac1{y} \, \textrm{d}y &= \int 1 \, \textrm{d}x \\ &\Rightarrow& \ln |y| &= x + \ln A \\ &\Rightarrow& \ln \frac{ |y| }{ A } &= x \\ &\Rightarrow& \frac{ |y| }{ A } &= \textrm{e}^x \\ &\Rightarrow& |y| &= A \textrm{e}^x, \quad A>0 \\ \\ &\Rightarrow& y &= A \textrm{e}^x \quad \textrm{where} \quad A \in \mathbb R \end{align} $$
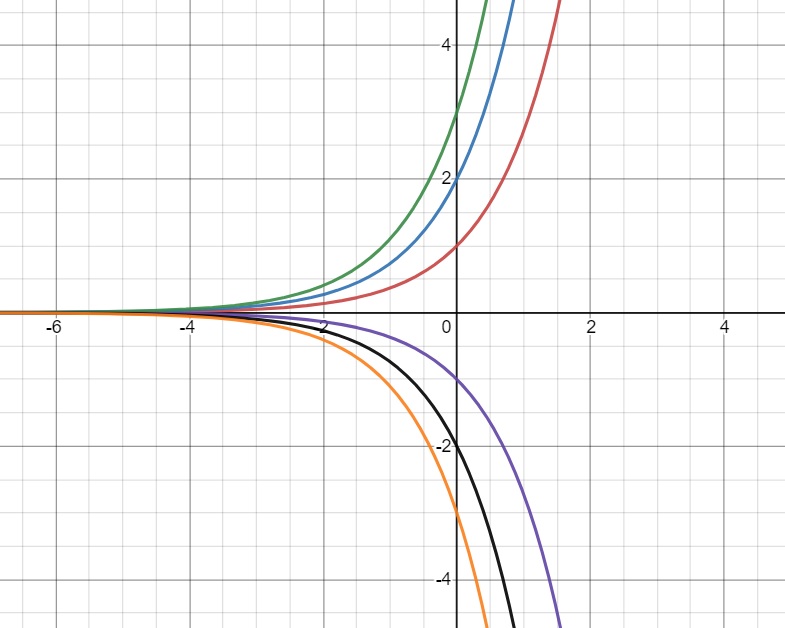
(c)
$$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= \frac{2y}{x} \\ &\Rightarrow& \frac{1}{y}\frac{ \textrm{d}y }{ \textrm{d}x } &= \frac{2}{x} \\ &\Rightarrow& \int \frac1{y} \, \textrm{d}y &= \int \frac{2}{x} \, \textrm{d}x \\ &\Rightarrow& \ln |y| &= 2 \ln |x| + \ln A = \ln A|x|^2 \\ &\Rightarrow& |y| &= Ax^2, \quad A>0 \\ \\ &\Rightarrow& y &= A x^2 \quad \textrm{where} \quad A \in \mathbb R \end{align} $$
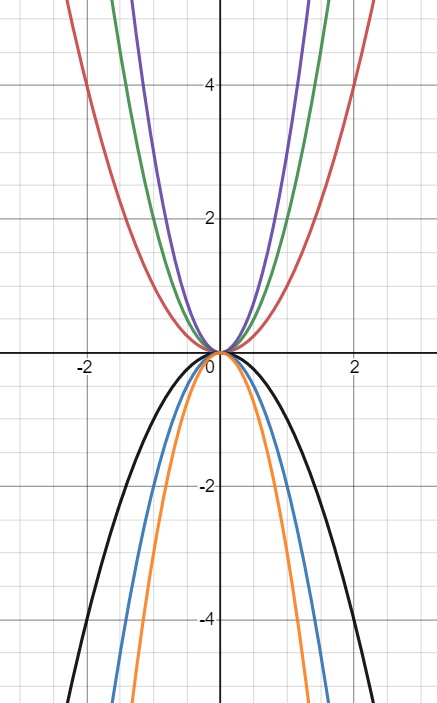
(d)
$$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= \frac{x}{y} \\ &\Rightarrow& y\frac{ \textrm{d}y }{ \textrm{d}x } &= x \\ &\Rightarrow& \int y\, \textrm{d}y &= \int x \, \textrm{d}x \\ &\Rightarrow& \frac12 y^2 &= \frac12 x^2 - \frac12 C \\ \\ &\Rightarrow& x^2 - y^2 &= C \end{align} $$
which yields a family of hyperbolae.
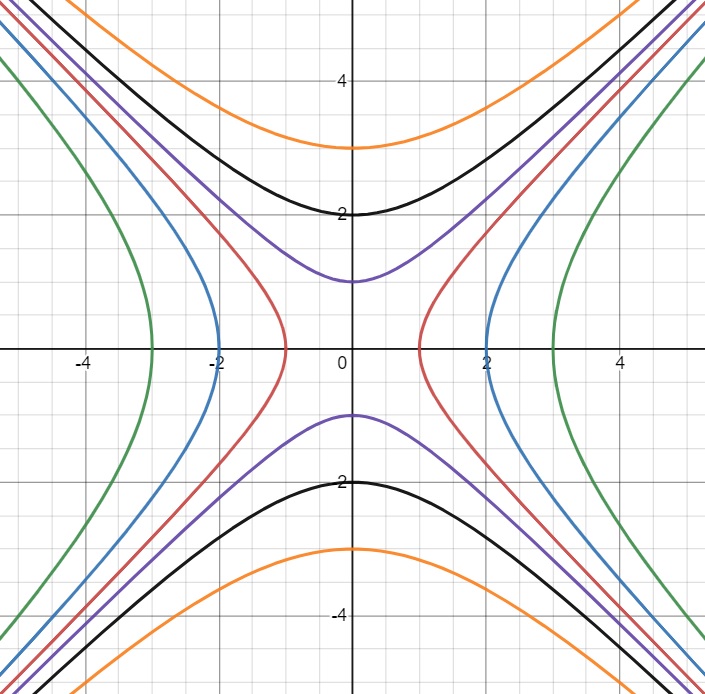
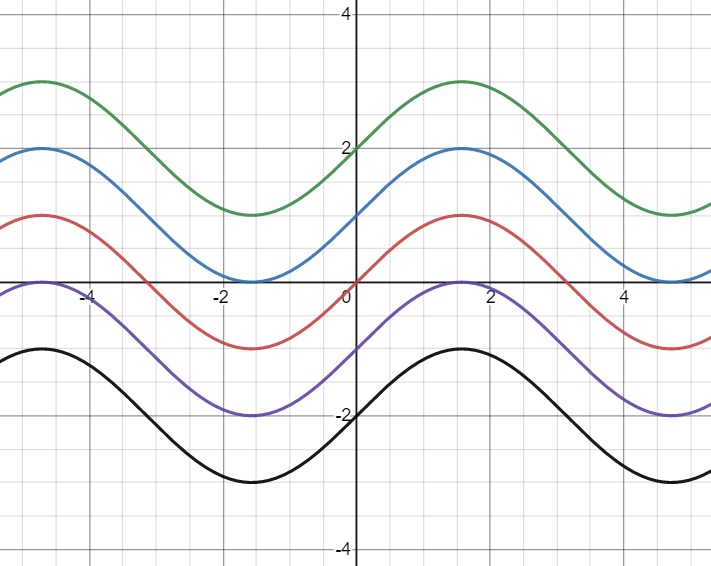
(e)
$$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= \cos x \\ &\Rightarrow& y &= \int \cos x \, \textrm{d}x \\ &&&= \sin x + C \end{align} $$
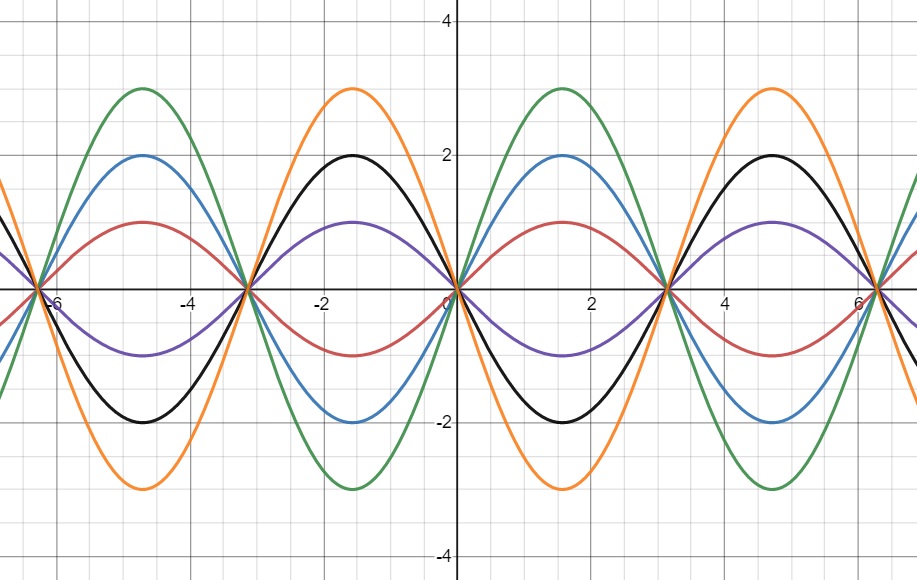
(f)
$$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= y \cot x \\ &\Rightarrow& \frac{1}{y}\frac{ \textrm{d}y }{ \textrm{d}x } &= \cot x \\ &\Rightarrow& \int \frac1{y} \, \textrm{d}y &= \int \frac{ \cos x }{ \sin x } \, \textrm{d}x \\ &\Rightarrow& \ln |y| &= \ln \sin x + \ln A \qquad (\textrm{since} \quad 0 < x < \pi) \\ &\Rightarrow& |y| &= A \sin x, \quad A>0 \\ \\ &\Rightarrow& y &= A \sin x \quad \textrm{where} \quad A \in \mathbb R \end{align} $$
Question 2. Given that $k$ is an arbitrary positive constant,(a) show that $y^2 + kx^2 = 9k$ is the general solution to the differential equation
$$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } = - \frac{ xy }{ 9 - x^2 }, \qquad |x| < 3 \end{align} $$(b) find the particular solution, which passes through the point $(2,5)$
(c) sketch the family of solution curves for $k=\frac19, \frac49,1$ and include your particular solution in the diagram.
Solution.
(a) $$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } = - \frac{ xy }{ 9 - x^2 } \\ &\Rightarrow& \frac1y \frac{ \textrm{d}y }{ \textrm{d}x } &= - \frac{ x }{ 9 - x^2 } \\ &\Rightarrow& \int \frac1y \, \textrm{d}y &= - \int \frac{ x }{ 9 - x^2 } \, \textrm{d}x \\ &\Rightarrow& \ln |y| &= \frac12 \ln \left( 9 - x^2 \right) + \frac12 k \\ &\Rightarrow& 2\ln |y| = \ln |y|^2 &= \ln k\left( 9 - x^2 \right) \\ \\ &\Rightarrow& y^2 &= 9k - k x^2 \qquad \square \end{align} $$ where $k$ is an arbitrary constant.
Comment: This is a family of ellipses: $$ \begin{align} kx^2 + y^2 = 9k \frac{ x^2 }{ 9 } + \frac{ y^2 }{ k } = 1 \end{align} $$ with the $y$-intercepts $\left( 0, \pm \sqrt{k} \right)$ being arbitrary.
(b) Apply the boundary condition $(2,5)$, $$ \begin{align} y^2 + kx^2 &= 9k \\ \\ (2,5)\; : \qquad 5^2 + 2^2k &= 9k \qquad \Rightarrow \qquad k = 5 \end{align} $$ so the particular solution is: $$ \begin{align} 5x^2 + y^2 = 45 \qquad \Leftrightarrow \qquad \frac{ x^2 }{ 9 } + \frac{ y^2 }{ 5 } = 1 \end{align} $$ This is an ellipse passing through $\left( \pm 3, 0 \right)$ and $\left( 0, \pm \sqrt{5} \right)$.
(c) The diagram below shows the four curves with $$ \begin{align} k &= \frac19 \; ( \textrm{red} ) \\ k &= \frac49 \; ( \textrm{blue} ) \\ k &= 1 \; ( \textrm{purple} ) \\ k &= 5 \; ( \textrm{black} ) \end{align} $$
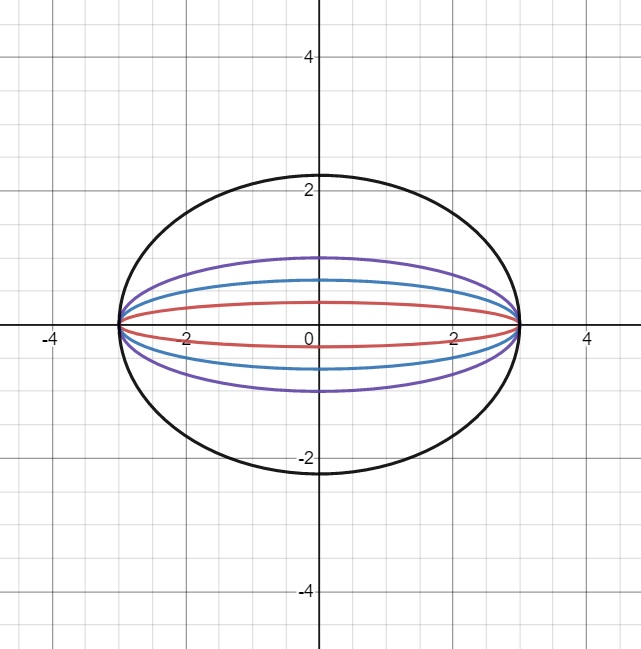
Question 3. Find the general solutions to these differential equations. $$ \begin{align} \textbf{(a)}&&& x \frac{ \textrm{d}y }{ \textrm{d}x } + y = \cos x &&& \textbf{(b)}&&& \textrm{e}^{-x} \frac{ \textrm{d}y }{ \textrm{d}x } - \textrm{e}^{-x} y = x \textrm{e}^{x} \\ \\ \textbf{(c)}&&& \sin x \frac{ \textrm{d}y }{ \textrm{d}x } + y \cos x = 3 &&& \textbf{(d)}&&& \frac1x \frac{ \textrm{d}y }{ \textrm{d}x } - \frac1{x^2}y = \textrm{e}^x \\ \\ \textbf{(e)}&&& x^2 \textrm{e}^{y} \frac{ \textrm{d}y }{ \textrm{d}x } + 2x \textrm{e}^{y} = x &&& \textbf{(f)}&&& 4xy \frac{ \textrm{d}y }{ \textrm{d}x } + 2y^2 = x^2 \end{align} $$
Solution.
(a) $$ \begin{align} && x \frac{ \textrm{d}y }{ \textrm{d}x } + y &= \cos x \\ &\Rightarrow& \frac{ \textrm{d}y }{ \textrm{d}x } (xy) &= \cos x \\ &\Rightarrow& xy &= \int \cos x \, \textrm{d}x = \sin x + C \\ \\ &\Rightarrow& y &= \frac{ \sin x }{ x } + \frac{ C }{ x } \end{align} $$
(b) $$ \begin{align} && \textrm{e}^{-x} \frac{ \textrm{d}y }{ \textrm{d}x } - \textrm{e}^{-x} y &= x \textrm{e}^{x} \\ &\Rightarrow& \frac{ \textrm{d}y }{ \textrm{d}x } \left( \textrm{e}^{-x} y \right) &= x \textrm{e}^{x} \\ &\Rightarrow& \textrm{e}^{-x} y &= \int x \textrm{e}^{x} \, \textrm{d}x \end{align} $$ We use integration by parts for the right-hand side, $$ \begin{align} u &= x, & v' &= \textrm{e}^{x} \\ u' &= 1, & v &= \textrm{e}^{x} \end{align} $$ which gives $$ \begin{align} \int x \textrm{e}^{x} \, \textrm{d}x &= x \textrm{e}^{x} - \int \textrm{e}^{x} \, \textrm{d}x \\ &= x \textrm{e}^{x} - \textrm{e}^{x} + C \end{align} $$ Finally, the general solution reads: $$ \begin{align} y &= \textrm{e}^{x} \int x \textrm{e}^{x} \, \textrm{d}x \\ &= \textrm{e}^{x} \left( x \textrm{e}^{x} - \textrm{e}^{x} + C \right) \\ &= ( x - 1 ) \textrm{e}^{2x} + C \textrm{e}^{x} \end{align} $$
(c) $$ \begin{align} && \sin x \frac{ \textrm{d}y }{ \textrm{d}x } + y \cos x &= 3 \\ &\Rightarrow& \frac{ \textrm{d}y }{ \textrm{d}x } \Big[ (\sin x) y \Big] &= 3 \\ &\Rightarrow& \sin x \, y &= \int 3 \, \textrm{d}x = 3 x + C \\ \\ &\Rightarrow& y &= \frac{ 3 x + C }{ \sin x } \end{align} $$
(d) $$ \begin{align} && \frac1x \frac{ \textrm{d}y }{ \textrm{d}x } - \frac1{x^2}y &= \textrm{e}^x \\ &\Rightarrow& \frac{ \textrm{d}y }{ \textrm{d}x } \left( \frac1{x} y \right) &= \textrm{e}^x \\ &\Rightarrow& \frac1{x} y &= \int \textrm{e}^x \, \textrm{d}x = \textrm{e}^x + C \\ \\ &\Rightarrow& y &= x \left( \textrm{e}^x \right) + Cx \end{align} $$
(e) $$ \begin{align} && x^2 \textrm{e}^{y} \frac{ \textrm{d}y }{ \textrm{d}x } + 2x \textrm{e}^{y} &= x \\ &\Rightarrow& \frac{ \textrm{d}y }{ \textrm{d}x } \left( x^2 \textrm{e}^{y} \right) &= x \\ &\Rightarrow& x^2 \textrm{e}^{y} &= \int x \, \textrm{d}x = \frac12 x^2 + C \\ &\Rightarrow& \textrm e^y &= \frac12 + \frac{ C }{ x^2 } \qquad (\textrm{with} \; C>0) \\ \\ &\Rightarrow& y &= \ln \left( \frac12 + \frac{ C }{ x^2 } \right) \quad \textrm{where} \quad C > 0 \end{align} $$
(f) $$ \begin{align} && 4xy \frac{ \textrm{d}y }{ \textrm{d}x } + 2y^2 &= x^2 \\ &\Rightarrow& \frac{ \textrm{d}y }{ \textrm{d}x } \left( 2x y^2 \right) &= x^2 \\ &\Rightarrow& 2x y^2 &= \int x^2 \, \textrm{d}x = \frac13 x^3 + C \\ \\ &\Rightarrow& y^2 &= \frac16 x^2 + \frac{ C }{ 2x } \end{align} $$
Question 4. (E)
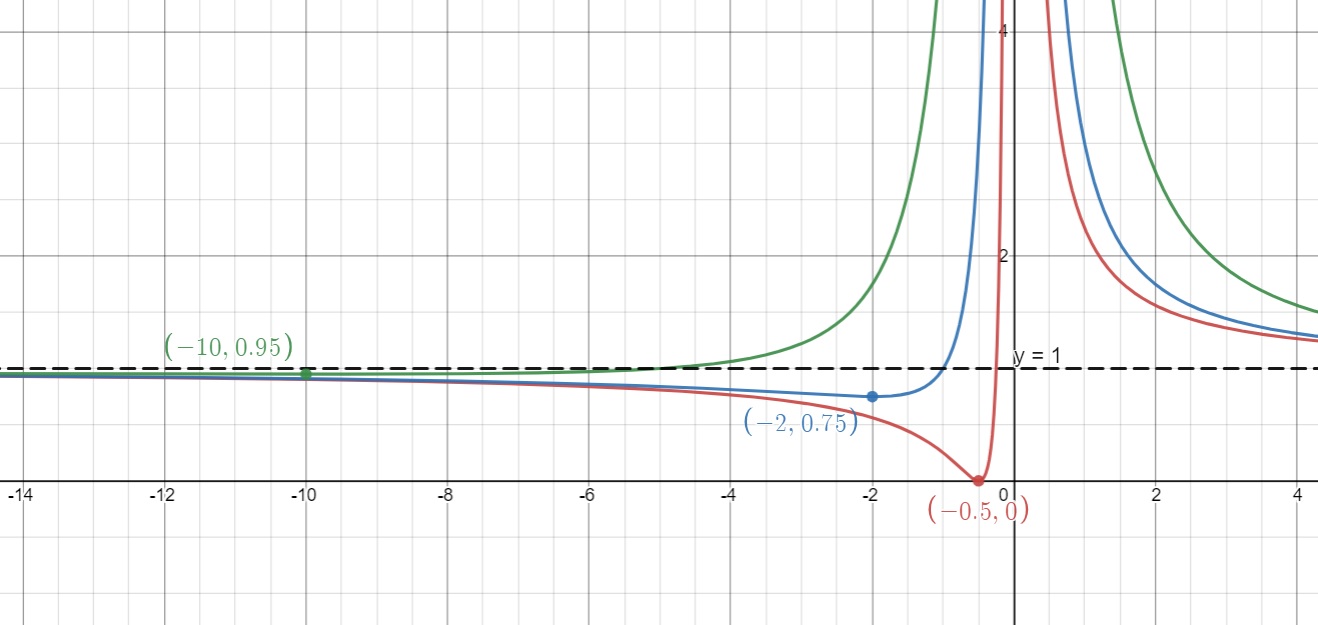
(a) [4 marks] Find the general solution to the differential equation $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + 2xy = \textrm{e}^{-x^2} \end{align} $$ (b) Describe the behaviour of $y$ as $x \rightarrow \infty$. [1 mark]
Solution.
(a) The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ \int 2x \, \textrm{d}x } = \textrm{e}^{x^2} \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & \textrm{e}^{x^2} \frac{ \textrm{d}y }{ \textrm{d}x } + 2x \textrm{e}^{x^2} y &= \textrm{e}^{x^2} \textrm{e}^{-x^2}=1 \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ \textrm{e}^{x^2} y \Big] &= 1 \\ & \Rightarrow & \textrm{e}^{x^2} y &= \int 1 \, \textrm{d}x = x + C \\ \\ & \Rightarrow & y &= ( x + C ) \textrm{e}^{ - x^2 } \end{align} $$
(b) As $x \rightarrow \infty$, the exponential term dominates and it vanishes to zero, i.e. $y \rightarrow 0$.
Aside. The stationary points are given by: $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } = \textrm{e}^{ - x^2 } + -2x (x+C) \textrm{e}^{ - x^2 } = \left( 1 - 2C x - 2x^2 \right) \textrm{e}^{ - x^2 } = 0 \end{align} $$ This gives $$ \begin{align} 2x^2 + 2C x - 1 = 0 \qquad \Rightarrow \qquad x = \frac{ - C \pm \sqrt{ C^2 + 2 } }{ 2 } \end{align} $$ So there are always two stationary points, a local maximum and a local minimum.
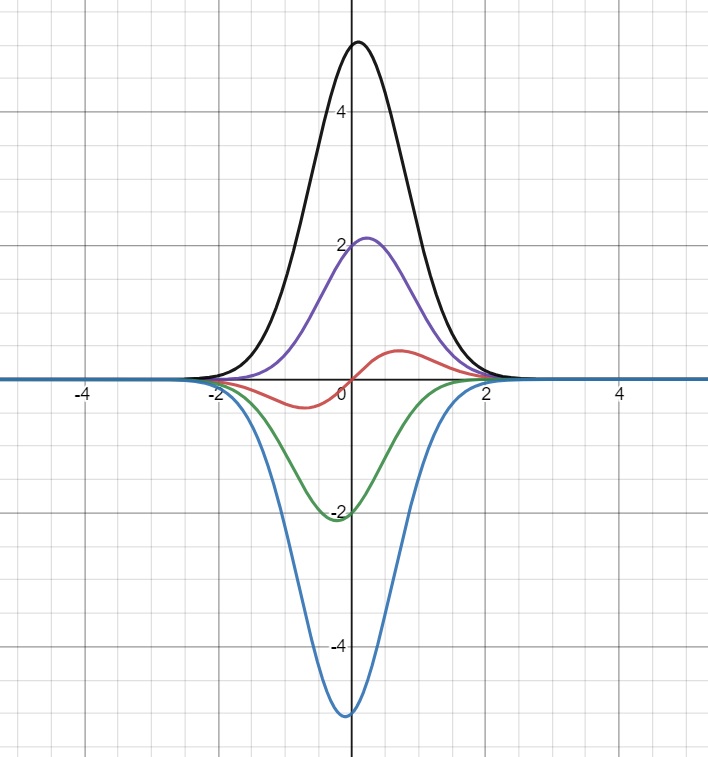
Question 5. (a) Find the general solution to the differential equation $$ \begin{align} x^2 \frac{ \textrm{d}y }{ \textrm{d}x } + 2xy = 2x + 1 \end{align} $$ (b) Find the three particular solutions which pass through the points with coordinates $\left( -\frac12,0 \right)$, $\left( -\frac12,3\right)$ and $\left( -\frac12,19\right)$ respectively and sketch their solution curves for $x < 0$.
Solution.
(a) We start with dividing the differential equation by $\textrm a(x)=x^2$: $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac2x y = \frac{ 2x + 1 }{ x^2 } \end{align} $$ The integrating factor reads: $$ \begin{align} \textrm f(x) &= \textrm{e}^{ \int \frac2x \, \textrm{d}x } \\ &= \textrm{e}^{ 2 \ln | x | } \\ &= x^2 \end{align} $$ As we multiply the differential equation by the integrating factor, we find: (it turns out that the original equation was already in the form of an exact derivative of a product) $$ \begin{align} & \Rightarrow & x^2 \frac{ \textrm{d}y }{ \textrm{d}x } + 2xy &= 2x + 1 \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ x^2 y \Big] &= 2x + 1 \\ & \Rightarrow & x^2 y &= \int ( 2x + 1 ) \, \textrm{d}x = x^2 + x + C \\ \\ & \Rightarrow & y &= 1 + \frac1x + \frac{ C }{ x^2 } \end{align} $$
(b) We apply the boundary condition(s): $$ \begin{align} \textrm{(i)}&& \left( -\frac12,0 \right)& \; : & 0 &= 1 - 2 + \frac{ C }{ \frac14 } \\ &&&& \Rightarrow \quad C &= \frac14 \\ &&&& \Rightarrow \quad y &= 1 + \frac1x + \frac{ 1 }{ 4 x^2 } \\ \\ \textrm{(ii)}&& \left( -\frac12,3\right)& \; : & 3 &= 1 - 2 + \frac{ C }{ \frac14 } \\ &&&& \Rightarrow \quad C &= 1 \\ &&&& \Rightarrow \quad y &= 1 + \frac1x + \frac{ 1 }{ x^2 } \\ \\ \textrm{(iii)}&& \left( -\frac12,19\right)& \; : & 19 &= 1 - 2 + \frac{ C }{ \frac14 } \\ &&&& \Rightarrow \quad C &= 5 \\ &&&& \Rightarrow \quad y &= 1 + \frac1x + \frac{ 5 }{ x^2 } \end{align} $$
Aside. The stationary points are given by: $$ \begin{align} && \textrm f(x) &= 1 + \frac1x + \frac{ C }{ x^2 } \\ \\ &\Rightarrow& \textrm f'(x) &= - \frac1{ x^2 } - \frac{ 2C }{ x^3 } = - \frac{ x + 2C }{ x^3 } = 0 \\ \end{align} $$ We have $$ \begin{align} \textrm f(-2C) &= 1 - \frac1{2C} + \frac{ C }{ 4C^2 } \\ &= 1 - \frac1{2C} + \frac{ 1 }{ 4C } \\ &= 1 - \frac1{4C} \\ \\ \textrm f''(x) &= \frac2{ x^3 } + \frac{ 6C }{ x^4 } \\ \textrm f''(-2C) &= - \frac2{ 8C^3 } + \frac{ 6C }{ 16C^4 } \\ &= - \frac2{ 8C^3 } + \frac{ 3 }{ 8C^3 } \\ &= \frac1{ 8C^3 } \end{align} $$ So the stationary point is at $$ \left( -2C, 1 - \frac1{4C} \right) $$ and it is:
- a local minimum for $C>0$,
- a local maximum for $C<0$.
- When $C=0$, the seemingly 'stationary point' coincides with the singularity.
Question 6. (a) Find the general solution to the differential equation $$ \begin{align} \ln x \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{y}{x} = \frac1{(x+1)(x+2)}, \qquad x>1 \end{align} $$ (b) Find the particular solution which passes through the point $(2,2)$.
Solution.
(a) We notice that the left-hand side is an exact derivative of a product, $$ \begin{align} \frac{ \textrm{d} }{ \textrm{d}x } \Big[ (\ln x) y \Big] &= \frac1{ (x+1)(x+2) } \\ (\ln x) y &= \int \frac1{ (x+1)(x+2) } \, \textrm{d}x \end{align} $$ For the integral on the right-hand side, we use the method of partial fractions. $$ \begin{align} \frac1{ (x+1)(x+2) } = \frac1{ x + 1 } - \frac1{ x + 2 } \\ \\ \Rightarrow \qquad \int \frac1{ (x+1)(x+2) } \, \textrm{d}x &= \int \left( \frac1{ x + 1 } - \frac1{ x + 2 } \right) \, \textrm{d}x \\ &= \ln |x+1| - \ln |x+2| + C \\ &= \ln \left\vert \frac{x+1}{x+2} \right\vert + C \end{align} $$ Then, the general solution reads $$ \begin{align} &\Rightarrow& (\ln x) y &= \ln \left( \frac{x+1}{x+2} \right) + C \qquad (\textrm{since} \, x > 1) \\ \\ &\Rightarrow& y &= \frac1{ \ln x }\ln \left( \frac{x+1}{x+2} \right) + \frac{ C }{ \ln x } = \frac{ \ln \left[ C \left( \frac{x+1}{x+2} \right) \right] }{ \ln x } \end{align} $$
Aside. We can alternatively find the integrating factor: $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{y}{ x \ln x } = \frac1{ (\ln x) (x+1)(x+2) } \end{align} $$ The integrating factor reads, with the substitution $t = \ln x$ and $\textrm dt = \frac{\textrm dx}{x}$, $$ \begin{align} \textrm f(x) &= \textrm e^{ \int \frac1{ x \ln x } \, \textrm{d}x } \\ &= \textrm e^{ \int \frac1{ t } \, \textrm{d}t } \\ &= \textrm e^{ \ln t } \\ &= t \\ &= \ln x \end{align} $$ and this recovers the original differential equation.
(b) We apply the boundary condition $(2,2)$: $$ \begin{align} && 2 &= \frac{ \ln \left( \frac{3C}{4} \right) }{ \ln 2 } \\ &\Rightarrow& \ln \left( \frac{3C}{4} \right) &= 2 \ln 2 = \ln 4 \\ &\Rightarrow& \frac{3C}{4} &= 4 \qquad (\textrm{since log is a 1-to-1 function}) \\ &\Rightarrow& C &= \frac{16}{3} \end{align} $$ and the particular solution reads $$ \begin{align} y = \frac{ \ln \left[ \frac{ 16(x+1) }{ 3(x+2) } \right] }{ \ln x } \end{align} $$
Question 7. Find the general solutions to these differential equations by using an integrating factor. $$ \begin{align} \textbf{(a)}&&& \frac{ \textrm{d}y }{ \textrm{d}x } + 2y = \textrm{e}^x & \textbf{(b)}&&& \frac{ \textrm{d}y }{ \textrm{d}x } + y \cot x = 1 \\ \\ \textbf{(c)}&&& \frac{ \textrm{d}y }{ \textrm{d}x } + y \sin x = \textrm{e}^{\cos x} & \textbf{(d)}&&& \frac{ \textrm{d}y }{ \textrm{d}x } - y = \textrm{e}^{2x} \\ \\ \textbf{(e)}&&& \frac{ \textrm{d}y }{ \textrm{d}x } + y \tan x = x \cos x & \textbf{(f)}&&& \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{y}{x} = \frac1{x^2} \\ \\ \textbf{(g)}&&& x^2 \frac{ \textrm{d}y }{ \textrm{d}x } - x y = \frac{ x^3 }{ x+2 }, \quad x>-2 & \textbf{(h)}&&& 3x \frac{ \textrm{d}y }{ \textrm{d}x } + y = x \\ \\ \textbf{(i)}&&& (x+2) \frac{ \textrm{d}y }{ \textrm{d}x } - y = x + 2 & \textbf{(j)}&&& x \frac{ \textrm{d}y }{ \textrm{d}x } + 4 y = \frac{ \textrm{e}^x }{ x^2 } \end{align} $$
Solution.
(a)
$$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + 2y = \textrm{e}^x \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ \int 2 \, \textrm{d}x } = \textrm{e}^{2x} \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & \textrm{e}^{ 2x } \frac{ \textrm{d}y }{ \textrm{d}x } + 2\textrm{e}^{ 2x } y &= \textrm{e}^{ 2x } \textrm{e}^x \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ \textrm{e}^{ 2x } y \Big] &= \textrm{e}^{ 3x } \\ & \Rightarrow & \textrm{e}^{ 2x } y &= \int \textrm{e}^{ 3x } \, \textrm{d}x = \frac13 \textrm{e}^{ 3x } + C \\ \\ & \Rightarrow & y &= \frac13 \textrm{e}^x + C \textrm{e}^{-2x} \end{align} $$
(b)
$$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + y \cot x = 1 \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ \int \cot x \, \textrm{d}x } = \textrm{e}^{ \ln | \sin x | } = \sin x \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & \sin x \frac{ \textrm{d}y }{ \textrm{d}x } + (\cos x) y &= \sin x \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ (\sin x) y \Big] &= \sin x \\ & \Rightarrow & (\sin x) y &= \int \sin x \, \textrm{d}x = - \cos x + C \\ \\ & \Rightarrow & y &= - \cot x + C \csc x \end{align} $$
(c)
$$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + y \sin x = \textrm{e}^{\cos x} \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ \int \sin x \, \textrm{d}x } = \textrm{e}^{-\cos x} \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} && \textrm{e}^{-\cos x} \frac{ \textrm{d}y }{ \textrm{d}x } + \left( \sin x \textrm{e}^{-\cos x} \right) y &= \textrm{e}^{-\cos x} \textrm{e}^{\cos x} \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ \textrm{e}^{-\cos x} y \Big] &= 1 \\ & \Rightarrow & \textrm{e}^{-\cos x} y &= \int 1 \, \textrm{d}x = x + C \\ \\ & \Rightarrow & y &= ( x + C ) \textrm{e}^{\cos x} \end{align} $$
(d)
$$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } - y = \textrm{e}^{2x} \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ - \int 1 \, \textrm{d}x } = \textrm{e}^{-x} \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} && \textrm{e}^{-x} \frac{ \textrm{d}y }{ \textrm{d}x } - \textrm{e}^{-x} y &= \textrm{e}^{-x} \textrm{e}^{2x} \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ \textrm{e}^{ - x } y \Big] &= \textrm{e}^{ x } \\ & \Rightarrow & \textrm{e}^{ - x } y &= \int \textrm{e}^{ x } \, \textrm{d}x = \textrm{e}^{ x } + C \\ \\ & \Rightarrow & y &= \textrm{e}^{ 2x } + C \textrm{e}^{x} \end{align} $$
(e)
$$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + y \tan x = x \cos x \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ \int \tan x \, \textrm{d}x } = \textrm{e}^{ \ln | \sec x | } = \sec x = \frac1{\cos x} \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} && \frac1{\cos x} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{ \sin x }{ \cos^2 x} y &= x \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \left[ \frac1{\cos x} y \right] &= x \\ & \Rightarrow & \frac1{\cos x} y &= \int x \, \textrm{d}x = \frac12 x^2 + \frac12 C \\ \\ & \Rightarrow & y &= \frac12 \left( x^2 + C \right) \cos x \end{align} $$
(f)
$$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{y}{x} = \frac1{x^2} \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ \int \frac1x \, \textrm{d}x } = \textrm{e}^{ \ln |x| } = x \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} && x \frac{ \textrm{d}y }{ \textrm{d}x } + y &= \frac1{x} \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ x y \Big] &= \frac1{ x } \\ & \Rightarrow & x y &= \int \frac1x \, \textrm{d}x = \ln |x| + C \\ \\ & \Rightarrow & y &= \frac{ \ln |x| + C }{ x } \end{align} $$
(g)
$$ \begin{align} x^2 \frac{ \textrm{d}y }{ \textrm{d}x } - x y = \frac{ x^3 }{ x+2 }, \quad x>-2 \end{align} $$ We start with dividing the equation by $\textrm a(x)=x^2$, $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } - \frac1x y = \frac{ x }{ x+2 }, \quad x>-2 \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ - \int \frac1x \, \textrm{d}x } = \textrm{e}^{ - \ln |x| } = \frac1x \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} && \frac1x \frac{ \textrm{d}y }{ \textrm{d}x } - \frac1{ x^2 } y &= \frac{ 1 }{ x+2 } \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ \frac1x y \Big] &= \frac{ 1 }{ x + 2 } \\ & \Rightarrow & \frac1x y &= \int \frac{ 1 }{ x+2 } \, \textrm{d}x = \ln | x + 2 | + C \\ \\ & \Rightarrow & y &= x \ln | x + 2 | + C x \end{align} $$
(h)
$$ \begin{align} 3x \frac{ \textrm{d}y }{ \textrm{d}x } + y = x \end{align} $$ We start with dividing the equation by $\textrm a(x)=3x$, $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac1{3x} y = \frac13 \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ \int \frac1{3x} \, \textrm{d}x } = \textrm{e}^{ \frac13 \ln |x| } = x^{\frac13} \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} && x^{\frac13} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac13 x^{-\frac23} y &= \frac13 x^{\frac13} \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \left[ x^{\frac13} y \right] &= \frac13 x^{\frac13} \\ & \Rightarrow & x^{\frac13} y &= \int \frac13 x^{\frac13} \, \textrm{d}x = \frac14 x^{\frac43} + C \\ \\ & \Rightarrow & y &= \frac14 x + C x^{-\frac13} \end{align} $$
(i)
$$ \begin{align} (x+2) \frac{ \textrm{d}y }{ \textrm{d}x } - y = x + 2 \end{align} $$ We start with dividing the equation by $\textrm a(x)=x+2$, $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } - \frac1{x+2} y = 1 \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ - \int \frac1{x+2} \, \textrm{d}x } = \textrm{e}^{-\ln |x+2|} = \frac1{x+2} \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} && \frac1{x+2} \frac{ \textrm{d}y }{ \textrm{d}x } - \frac1{(x+2)^2} y &= \frac1{x+2} \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ \frac1{x+2} y \Big] &= \frac1{x+2} \\ & \Rightarrow & \frac1{x+2} y &= \int \frac1{x+2} \, \textrm{d}x = \ln | x + 2 | + C \\ \\ & \Rightarrow & y &= (x+2) \ln |x+2| + C (x+2) \end{align} $$
(j)
$$ \begin{align} x \frac{ \textrm{d}y }{ \textrm{d}x } + 4 y = \frac{ \textrm{e}^x }{ x^2 } \end{align} $$ We start with dividing the equation by $\textrm a(x)=x$, $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac4{x} y = \frac{ \textrm{e}^x }{ x^3 } \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ \int \frac4x \, \textrm{d}x } = \textrm{e}^{ 4 \ln |x| } = x^4 \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} && x^4 \frac{ \textrm{d}y }{ \textrm{d}x } + 4x^3 y = x \textrm{e}^x \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ x^4 y \Big] &= x \textrm{e}^x \\ & \Rightarrow & x^4 y &= \int x \textrm{e}^x \, \textrm{d}x \end{align} $$ For the last integral, we use integration by parts, $$ \begin{align} u &= x & v' &= \textrm{e}^x \\ u' &= 1 & v &= \textrm{e}^x \end{align} $$ and find: $$ \begin{align} \int x \textrm{e}^x \, \textrm{d}x &= x \textrm{e}^x - \int \textrm{e}^x \, \textrm{d}x \\ &= x \textrm{e}^x - \textrm{e}^x + C \end{align} $$ Finally, the general solution reads: $$ \begin{align} & \Rightarrow & x^4 y &= ( x - 1 ) \textrm{e}^x + C \\ \\ & \Rightarrow & y &= \frac{ ( x - 1 ) \textrm{e}^x + C }{ x^4 } \end{align} $$
Question 8. (E) Find $y$ in terms of $x$ given that $$ \begin{align} x \frac{ \textrm{d}y }{ \textrm{d}x } + 2 y = \textrm{e}^x \end{align} $$ and that $y=1$ when $x=1$. [8 marks]
Solution.
We start with dividing the differential equation by $\textrm a(x)=x$: $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac2x y = \frac{ \textrm{e}^x }{ x } \end{align} $$ The integrating factor reads: $$ \begin{align} \textrm f(x) &= \textrm{e}^{ \int \frac2x \, \textrm{d}x } \\ &= \textrm{e}^{ 2 \ln | x | } \\ &= x^2 \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & x^2 \frac{ \textrm{d}y }{ \textrm{d}x } + 2xy &= x \textrm{e}^x \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ x^2 y \Big] &= x \textrm{e}^x \\ & \Rightarrow & x^2 y &= \int x \textrm{e}^x \, \textrm{d}x \end{align} $$ We use integration by parts for the integral on the right-hand side, $$ \begin{align} u &= x, & v' &= \textrm{e}^x \\ u' &= 1, & v &= \textrm{e}^x \end{align} $$ and it gives $$ \begin{align} \int x \textrm{e}^x \, \textrm{d}x &= x \textrm{e}^x - \int \textrm{e}^x \, \textrm{d}x \\ &= x \textrm{e}^x - \textrm{e}^x + C \end{align} $$ Then, the general solution reads $$ \begin{align} y &= \frac1{ x^2 } \int x \textrm{e}^x \, \textrm{d}x \\ &= \frac1{ x^2 } \left( x \textrm{e}^x - \textrm{e}^x + C \right) \\ &= \frac{ x - 1 }{ x^2 } \textrm{e}^x + \frac{ C }{ x^2 } \end{align} $$ Now, we apply the boundary condition $(1,1)$ to specify the value of $C$: $$ \begin{align} 1 = C \end{align} $$ so the particular solution reads: $$ \begin{align} y &= \frac{ ( x - 1 ) \textrm{e}^x + 1 }{ x^2 } \end{align} $$
Question 9. (E) Solve the differential equation, giving $y$ in terms of $x$, where $$ \begin{align} x^3 \frac{ \textrm{d}y }{ \textrm{d}x } - x^2 y = 1 \end{align} $$ and $y=1$ at $x=1$. [8 marks]
Solution.
We start with dividing the differential equation by $\textrm a(x)=x^3$: $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } - \frac1x y = \frac{ 1 }{ x^3 } \end{align} $$ The integrating factor reads: $$ \begin{align} \textrm f(x) &= \textrm{e}^{ - \int \frac1x \, \textrm{d}x } \\ &= \textrm{e}^{ - \ln | x | } \\ &= \frac1x \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & \frac1x \frac{ \textrm{d}y }{ \textrm{d}x } - \frac1{x^2} y &= \frac{ 1 }{ x^4 } \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \left( \frac1x y \right) &= \frac{ 1 }{ x^4 } \\ & \Rightarrow & \frac1x y &= \int \frac{ 1 }{ x^4 } \, \textrm{d}x \\ &&&= - \frac1{3x^3} + C \\ \\ & \Rightarrow & y &= - \frac1{3x^2} + Cx \end{align} $$ Now, we apply the boundary condition $(1,1)$ to specify the value of $C$: $$ \begin{align} 1 = - \frac13 + C \qquad \Rightarrow \qquad C = \frac43 \end{align} $$ so the particular solution reads: $$ \begin{align} y &= - \frac1{x^2} + \frac43 x \end{align} $$
Question 10. (E)
(a) Find the general solution to the differential equation $$ \begin{align} \left( x + \frac1x \right) \frac{ \textrm{d}y }{ \textrm{d}x } + 2 y = 2 \left( x^2 + 1 \right)^2 \end{align} $$ giving $y$ in terms of $x$. [6 marks](b) Find the particular solution which satisfies the condition that $y=1$ at $x=1$. [2 marks]
Solution.
(a) We start with dividing the differential equation by $\textrm a(x)=x + \frac1x$: $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{ 2x }{ x^2 + 1 } y = 2 \left( x^2 + 1 \right)^2 \frac{ x }{ x^2 + 1 } = 2x \left( x^2 + 1 \right) \end{align} $$ The integrating factor reads: $$ \begin{align} \textrm f(x) &= \textrm{e}^{ \int \frac{ 2x }{ x^2 + 1 } \, \textrm{d}x } \\ &= \textrm{e}^{ \ln \left\vert x^2 + 1 \right\vert } \\ &= x^2 + 1 \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & \left( x^2 + 1 \right) \frac{ \textrm{d}y }{ \textrm{d}x } + 2x y &= 2x \left( x^2 + 1 \right)^2 \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ \left( x^2 + 1 \right) y \Big] &= 2x \left( x^2 + 1 \right)^2 \\ & \Rightarrow & \left( x^2 + 1 \right) y &= \int 2x \left( x^2 + 1 \right)^2 \, \textrm{d}x \\ &&&= \frac13 \left( x^2 + 1 \right)^3 + C \\ \\ & \Rightarrow & y &= \frac13 \left( x^2 + 1 \right)^2 + \frac{ C }{ x^2 + 1 } \end{align} $$
(b) We apply the boundary condition $(1,1)$: $$ \begin{align} && 1 = \frac13 \left( 1 + 1 \right)^2 + \frac{ C }{ 1 + 1 } &= \frac{3}{4} + \frac{C}{2} \\ & \Rightarrow & C &= \frac12 \end{align} $$ and find the particular solution: $$ \begin{align} y &= \frac13 \left( x^2 + 1 \right)^2 + \frac{ 1 }{ 2 \left( x^2 + 1 \right) } \end{align} $$
Question 11. (E)
(a) [6 marks] Find the general solution to the differential equation $$ \begin{align} \cos x \frac{ \textrm{d}y }{ \textrm{d}x } + y = 1, \qquad -\frac{\pi}{2} < x < \frac{\pi}{2} \end{align} $$(b) Find the particular solution which satisfies the condition that $y=2$ at $x=0$. [2 marks]
Solution.
(a) We start with dividing the differential equation by $\textrm a(x)=\cos x$: $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \sec x y = \sec x \end{align} $$ The integrating factor reads: $$ \begin{align} \textrm f(x) &= \textrm{e}^{ \int \sec x \, \textrm{d}x } \\ &= \textrm{e}^{ \ln | \sec x + \tan x | } \\ &= \sec x + \tan x \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & ( \sec x + \tan x )\frac{ \textrm{d}y }{ \textrm{d}x } + \sec x ( \sec x + \tan x ) y &= \sec x ( \sec x + \tan x ) \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ ( \sec x + \tan x ) y \Big] &= \sec x ( \sec x + \tan x ) \\ & \Rightarrow & ( \sec x + \tan x ) y &= \int \left( \sec^2 x + \sec x \tan x \right) \, \textrm{d}x \\ &&&= \tan x + \sec x + C \\ \\ & \Rightarrow & y &= 1 + \frac{ C }{ \sec x + \tan x } \end{align} $$
(b) We apply the boundary condition $(0,2)$: $$ \begin{align} 2 = 1 + \frac{ C }{ \sec 0 + \tan 0} = 1 + C \qquad \Rightarrow \qquad C = 1 \end{align} $$ and find the particular solution: $$ \begin{align} y &= 1 + \frac{ 1 }{ \sec x + \tan x } = 1 + \frac{ \cos x }{ 1 + \sin x } \end{align} $$
Question 12. (E/P) Find the general solution to the differential equation $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } = x \sqrt{ y^2 - 4 } \end{align} $$ [5 marks][Hint: For the integral of $\int \frac1{ \sqrt{ y^2 - 4 } }\, \textrm{d}y$, we can use the substitution $y=2\cosh u$. See CP2 §6.5 Integrating hyperbolic functions.]
Solution.
By the method of separable variables, $$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= x \sqrt{ y^2 - 4 } \\ &\Rightarrow& \frac1{ \sqrt{ y^2 - 4 } } \frac{ \textrm{d}y }{ \textrm{d}x } &= x \\ &\Rightarrow& \int \frac1{ \sqrt{ y^2 - 4 } } \, \textrm{d}y &= \int x \, \textrm{d}x = \frac12 x^2 + C \end{align} $$ For the left-hand side, we use the substitution: $$ \begin{align} y &= 2 \cosh u \\ \textrm{d}y &= 2\sinh u \, \textrm{d}u \end{align} $$ and $$ \begin{align} \int \frac1{ \sqrt{ y^2 - 4 } } \, \textrm{d}y &= \int \frac1{ \sqrt{ 4 \left( \cosh^2u - 1 \right) } } 2\sinh u \, \textrm{d}u \\ &= u + C \\ &= \textrm{arcosh} \left( \frac{y}{2} \right) + C \end{align} $$ Then, the general solution reads: $$ \begin{align} &\Rightarrow& \textrm{arcosh} \left( \frac{y}{2} \right) &= \frac12 x^2 + C \\ \\ &\Rightarrow& y &= 2 \cosh \left( \frac12 x^2 + C \right) \end{align} $$
Question 13. (E/P)
(a) [4 marks] Find the general solution to the differential equation $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } = y \cosh x \end{align} $$ (b) Find the particular solution which satisfies the condition that $y = \textrm{e}$ when $x=0$. [2 marks]
Solution.
(a) By the method of separable variables: $$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= y \cosh x \\ &\Rightarrow& \frac1y \frac{ \textrm{d}y }{ \textrm{d}x } &= \cosh x \\ &\Rightarrow& \int \frac1y \, \textrm{d}y &= \int \cosh x \, \textrm{d}x \\ &\Rightarrow& \ln |y| &= \sinh x + \ln A \\ &\Rightarrow& |y| &= A \textrm e^{ \sinh x } \quad \textrm{with} \quad A > 0 \\ \\ &\Rightarrow& y &= A \textrm e^{ \sinh x } \quad \textrm{where} \quad A \in \mathbb R \end{align} $$
(b) We apply the boundary condition $(0,\textrm e)$: $$ \begin{align} \textrm e &= A \textrm e^{ \sinh 0 } \qquad \Rightarrow \qquad A = \textrm e \end{align} $$ and find the particular solution: $$ \begin{align} y &= \textrm e \cdot \textrm e^{ \sinh x } = \textrm e^{ \sinh x + 1 } \end{align} $$
Question 14. (E/P)
(a) [4 marks] Find the general solution to the differential equation $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } = \sqrt{ 1 + y^2 } \end{align} $$ (b) Sketch the family of solution curves. [3 marks]
Solution.
(a) By the method of separable variables: $$ \begin{align} && \frac{ \textrm{d}y }{ \textrm{d}x } &= \sqrt{ 1 + y^2 } \\ &\Rightarrow& \frac1{ \sqrt{ 1 + y^2 } } \frac{ \textrm{d}y }{ \textrm{d}x } &= 1 \\ &\Rightarrow& \int \frac1{ \sqrt{ 1 + y^2 } } \, \textrm{d}y &= \int 1 \, \textrm{d}x = x + C \end{align} $$ For the integral on the left-hand side, we use the substitution: $$ \begin{align} y &= \sinh u \\ \textrm{d}y &= \cosh u \, \textrm{d}u \end{align} $$ and find: $$ \begin{align} \int \frac1{ \sqrt{ 1 + y^2 } } \, \textrm{d}y &= \int \frac1{ \sqrt{ 1 + sinh^2u } } \cosh u \, \textrm{d}u \\ &= u + C \\ &= \textrm{arsinh} \, y + C \end{align} $$ Then, the general solution reads: $$ \begin{align} &\Rightarrow& \textrm{arsinh} \, y &= x + C \\ \\ &\Rightarrow& y &= \sinh ( x + C ) \end{align} $$
(b)
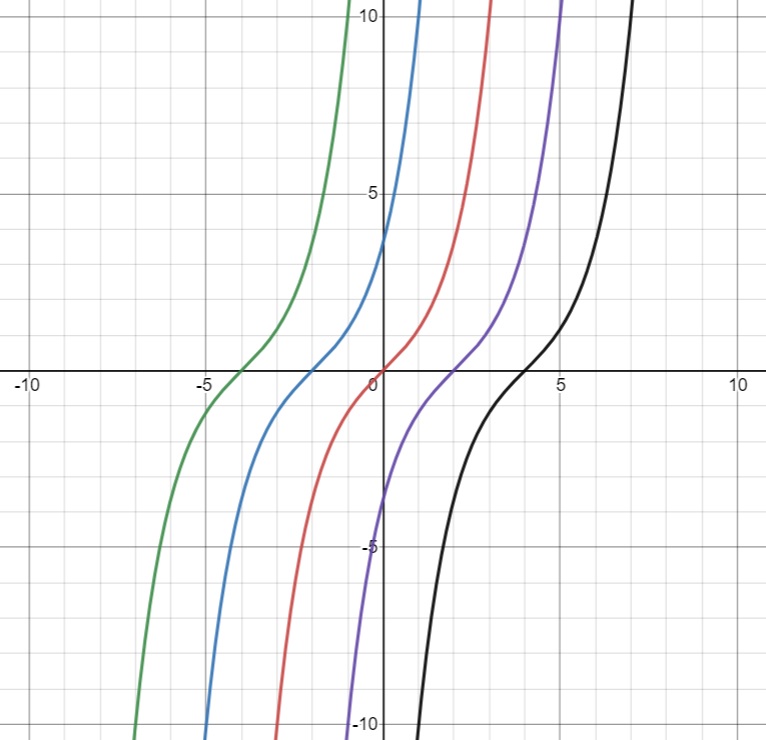
Question 15. (E)
(a) [6 marks] Find the general solution to the differential equation $$ \begin{align} \cos x \frac{ \textrm{d}y }{ \textrm{d}x } + y \sin x = 1 \end{align} $$(b) Find the particular solution such that $y=3$ when $x = \pi$. [2 marks]
(c) Show that the points $\left( \frac{ \pi }{ 2 }, 1 \right)$ and $\left( \frac{ 3 \pi }{ 2 }, -1 \right)$ lie on all possible solution curves. [3 marks]
Solution.
(a) We start with dividing the differential equation by $\textrm a(x)=\cos x$: $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{ \sin x }{ \cos x } y = \frac1{ \cos x } \end{align} $$ The integrating factor reads: $$ \begin{align} \textrm f(x) &= \textrm{e}^{ \int \frac{ \sin x }{ \cos x } \, \textrm{d}x } \\ &= \textrm{e}^{ - \ln |\cos x| } \\ &= \sec x \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & \frac{1}{\cos x} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{ \sin x }{ \cos^2 x } y &= \frac1{ \cos^2 x } \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \left[ \frac{1}{\cos x} y \right] &= \sec^2x \\ & \Rightarrow & \frac{1}{\cos x} y &= \int \sec^2 x \, \textrm{d}x \\ &&&= \tan x + A \\ \\ & \Rightarrow & y &= \sin x + A \cos x \end{align} $$
(b) We apply the boundary condition $(\pi, 3)$: $$ \begin{align} 3 = \sin \pi + A \cos \pi = - A \qquad \Rightarrow \qquad A = -3 \end{align} $$ and find the particular solution: $$ \begin{align} y &= \sin x - 3 \cos x \end{align} $$
Question 16. (E/P) Find a general solution to the equation $$ \begin{align} a \frac{ \textrm{d}y }{ \textrm{d}x } + b y = 0 \end{align} $$ in terms of $a$ and $b$. [6 marks]
Solution.
By the method of separable variables, $$ \begin{align} && a \frac{ \textrm{d}y }{ \textrm{d}x } &= - b y \\ &\Rightarrow& \frac1y \frac{ \textrm{d}y }{ \textrm{d}x } &= - \frac{b}{a} \\ &\Rightarrow& \int \frac1y \, \textrm{d}y &= - \int \frac{b}{a} \, \textrm{d}x \\ &\Rightarrow& \ln |y| &= - \frac{b}{a}x + \ln A \\ &\Rightarrow& |y| &= A \textrm e^{ - \frac{b}{a}x } \quad \textrm{with} \quad A > 0 \\ \\ &\Rightarrow& y &= A \textrm e^{ - \frac{b}{a}x } \quad \textrm{where} \quad A \in \mathbb R \end{align} $$
Aside. Alternatively, we can find the integrating factor. $$ \begin{align} \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{b}{a} y = 0 \end{align} $$ The integrating factor reads: $$ \begin{align} \textrm f(x) &= \textrm e^{ \int \frac{b}{a} \, \textrm{d}x } \\ &= \textrm e^{ \frac{b}{a} x } \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} &\Rightarrow& \textrm e^{ \frac{b}{a} x } \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{b}{a}\textrm e^{ \frac{b}{a} x } y = 0 \\ &\Rightarrow& \frac{ \textrm{d}y }{ \textrm{d}x } \left[ e^{ \frac{b}{a} x } y \right] &= 0 \\ &\Rightarrow& e^{ \frac{b}{a} x } y &= A \\ \\ &\Rightarrow& y &= A e^{ - \frac{b}{a} x } \qquad \checkmark \end{align} $$
8. First-order differential equations with constant coefficients
Question 16 above motivates us to consider the method of complementary function and particular integral, which will be our main tool for the second order differential equations in CP2 §7.2 Second-order homogeneous differential equations and §7.3 Second-order non-homogeneous differential equations. (The particular integrals are not to be confused with 'particular solutions'.)
8.1. First-order homogeneous differential equations
The equations of the form $$ \begin{align} a \frac{ \textrm{d}y }{ \textrm{d}x } + b y = 0 \end{align} $$ with 0 on the right-hand side are said to be first-oreder homogeneous differential equations with constant coefficients. The general solution is: $$ \begin{align} y = A \textrm{e}^{ - \frac{b}{a}x } \end{align} $$
8.2. First-order non-homogeneous differential equations
Now, we switch on $\textrm f(x)$ on the right hand side. The general solution consists of two parts, namely, complementary function and particular integral.
(i) The complementary function (C.F.) solves the corresponding homogeneous differential equation, i.e. $$ \begin{align} a \frac{ \textrm{d}y_1 }{ \textrm{d}x } + b y_1 = 0 \end{align} $$ (ii) The particular integral (P.I.) satisfies the inhomogeneous part, i.e. $$ \begin{align} a \frac{ \textrm{d}y_2 }{ \textrm{d}x } + b y_2 = \textrm f(x) \end{align} $$ The general solution is then: $$ \begin{align} y = y_1 + y_2 \end{align} $$
Comment: The fact that the general solution is the sum of $y_1$ and $y_2$ is due to the fact that the differential operator is linear, i.e. $$ \begin{align} \left( a \frac{ \textrm{d} }{ \textrm{d}x } + b \right) y &= \left( a \frac{ \textrm{d} }{ \textrm{d}x } + b \right) ( y_1 + y_2 ) \\ &= \underbrace{ \left( a \frac{ \textrm{d} y_1 }{ \textrm{d}x } + b y_1 \right) }_{=0} + \underbrace{ \left( a \frac{ \textrm{d} y_2 }{ \textrm{d}x } + b y_2 \right) }_{=\textrm f(x)} = \textrm f(x). \qquad \square \end{align} $$
The form of the particular integral depends on the form of $\textrm f(x)$. We consider the following five cases.
| $\textrm f(x)$ | Form of the particular integral |
| $p$ | $\lambda$ |
| $p + qx$ | $\lambda + \mu x$ |
| $p + qx + rx^2$ | $\lambda + \mu x + \nu x^2$ |
| $p \textrm{e}^{kx}$ | $\lambda \textrm{e}^{kx}$ |
| $p \cos \omega x + q \sin \omega x$ | $\lambda \cos \omega x + \mu \sin \omega x$ |
(i) $\textrm f(x) = p$ (constant).
Let $y=\lambda$. $$ \begin{align} a \frac{ \textrm{d}y }{ \textrm{d}x } + b y = p \\ b \lambda = p \\ \lambda = \frac{p}{b} \end{align} $$ So the general solution is: $$ \begin{align} a \frac{ \textrm{d}y }{ \textrm{d}x } + b y = p \qquad \Rightarrow \qquad y = A \textrm{e}^{-\frac{b}{a}x} + \frac{p}{b} \end{align} $$
(ii) $\textrm f(x) = p+qx$ (linear).
Let $y=\lambda + \mu x$. $$ \begin{align} && a \frac{ \textrm{d}y }{ \textrm{d}x } + b y &= p + qx \\ && a \mu + b ( \lambda + \mu x ) &= p + qx \\ \end{align} $$ Equating the coefficients yields: $$ \begin{align} \left\{ \begin{array}{l} a \mu + b \lambda = p \\ b \mu = q \end{array} \right. \qquad \Rightarrow \qquad \left\{ \begin{array}{l} \mu = \frac{q}{b} \\ \lambda = \frac{ p - a\mu }{ b } = \frac{ p - a\frac{q}{b} }{ b } = \frac{ b p - a q }{ b^2 } \end{array} \right. \end{align} $$ So the general solution is: $$ \begin{align} a \frac{ \textrm{d}y }{ \textrm{d}x } + b y = p + qx \qquad \Rightarrow \qquad y = A \textrm{e}^{-\frac{b}{a}x} + \frac{ b p - a q }{ b^2 } + \frac{q}{b} x \end{align} $$
(iii) $\textrm f(x) = p+qx+rx^2$ (quadratic).
Let $y=\lambda + \mu x + \nu x^2$. $$ \begin{align} y &= \lambda + \mu x + \nu x^2 \\ y' &= \mu + 2 \nu x \end{align} $$ The differential equation gives $$ \begin{align} && a \frac{ \textrm{d}y }{ \textrm{d}x } + b y &= p+qx+rx^2 \\ &\Rightarrow& a ( \mu + 2 \nu x ) + b \left( \lambda + \mu x + \nu x^2 \right) &= p+qx+rx^2 \end{align} $$ Equating the coefficients yields: $$ \begin{align} \left\{ \begin{array}{l} a \mu + b \lambda = p \\ 2 a \nu + b \mu = q \\ b \nu = r \end{array} \right. \qquad \Rightarrow \qquad \left\{ \begin{array}{l} \nu = \frac{r}{b} \\ \mu = \frac1b \left( q - 2a \nu \right) = \frac1b \left( q - \frac{ 2ar }{b} \right) = \frac{ bq - 2ar }{ b^2 } \\ \lambda = \frac1b \left( p - a \mu \right) = \frac1b \left( p - a \frac{ bq - 2ar }{ b^2 } \right) = \frac{ b^2p - abq + 2a^2r }{ b^3 } \end{array} \right. \end{align} $$ So the general solution is: $$ \begin{align} a \frac{ \textrm{d}y }{ \textrm{d}x } + b y = p + qx + rx^2 \qquad \Rightarrow \qquad y = A \textrm{e}^{-\frac{b}{a}x} + \frac{ b^2p - abq + 2a^2r }{ b^3 } + \frac{ bq - 2ar }{ b^2 } x + \frac{r}{b} x^2 \end{align} $$
(iv) $\textrm f(x) = p \textrm{e}^{kx} $ (exponential).
Let $y=\lambda \textrm{e}^{kx}$. $$ \begin{align} a \frac{ \textrm{d}y }{ \textrm{d}x } + b y &= p \textrm{e}^{kx} \\ a \left( k\lambda \textrm{e}^{kx} \right) + b \lambda \textrm{e}^{kx} &= p \textrm{e}^{kx} \\ (ak+b)\lambda \textrm{e}^{kx} &= p \textrm{e}^{kx} \end{align} $$ There are two cases to consider.
Case 1. If $ak+b \ne 0$ (i.e. $k \ne -\frac{b}{a}$), we find $$ \begin{align} \lambda = \frac{p}{ak+b} \end{align} $$ So the general solution is: $$ \begin{align} a \frac{ \textrm{d}y }{ \textrm{d}x } + b y = p \textrm{e}^{-\frac{b}{a}x} \qquad \Rightarrow \qquad y = A \textrm{e}^{-\frac{b}{a}x} + \frac{p}{ak+b} \textrm{e}^{kx} \end{align} $$ Case 2. If $ak+b = 0$ (i.e. $k = -\frac{b}{a}$), then $y=A \textrm{e}^{kx}= A \textrm{e}^{-\frac{b}{a}x}$ is the complementary function and the particular integral is given by $y = \lambda x \textrm{e}^{kx}$ instead. $$ \begin{align} y &= \lambda x \textrm{e}^{kx} \\ \frac{ \textrm{d}y }{ \textrm{d}x } &= \lambda \textrm{e}^{kx} + \lambda k x \textrm{e}^{kx} = \lambda ( 1 + k x ) \textrm{e}^{kx} \end{align} $$ The differential equation yields $$ \begin{align} && a \frac{ \textrm{d}y }{ \textrm{d}x } + b y &= p \textrm{e}^{kx} \\ & \Rightarrow & a \lambda \left( 1 + k x \right) \textrm{e}^{kx} + b \lambda x \textrm{e}^{kx} &= p \textrm{e}^{kx} \\ & \Rightarrow & \Big[ a + \underbrace{ (ak + b) }_{=0} x \Big] \lambda \textrm{e}^{kx} &= p \textrm{e}^{kx} \\ \\ & \Rightarrow & \lambda &= \frac{p}{a} \end{align} $$ So the general solution is: $$ \begin{align} a \frac{ \textrm{d}y }{ \textrm{d}x } + b y = p \textrm{e}^{-\frac{b}{a}x} \qquad \Rightarrow \qquad y = A \textrm{e}^{-\frac{b}{a}x} + \frac{p}{a} x \textrm{e}^{-\frac{b}{a}x} \end{align} $$
Aside. Do we not need to check $y = \lambda x^2 \textrm{e}^{kx}$ and so on for the particular integral?
더보기More generally, $$ \begin{align} y &= \sum_{n=0}^\infty c_n x^n \textrm{e}^{ kx } \\ y' &= \sum_{n=1}^\infty n c_n x^{n-1} \textrm{e}^{ kx } + \sum_{n=0}^\infty k c_n x^n \textrm{e}^{ kx } \\ &= \sum_{n=0}^\infty (n+1) c_{n+1} x^{n} \textrm{e}^{ kx } + \sum_{n=0}^\infty k c_n x^n \textrm{e}^{ kx } \\ &= \sum_{n=0}^\infty \Big[ (n+1) c_{n+1} + k c_n \Big] x^n \textrm{e}^{ kx } \end{align} $$ The differential equation gives $$ \begin{align} && a \frac{ \textrm{d}y }{ \textrm{d}x } + b y &= p \textrm{e}^{kx} \\ & \Rightarrow & a \left( \sum_{n=0}^\infty \Big[ (n+1) c_{n+1} + k c_n \Big] x^n \textrm{e}^{ kx } \right) + b \left( \sum_{n=0}^\infty c_n x^n \textrm{e}^{ kx } \right) &= p \textrm{e}^{kx} \\ & \Rightarrow & \sum_{n=0}^\infty \Big[ a (n+1) c_{n+1} + \underbrace{ ( ak + b ) }_{=0} c_n \Big]x^n \textrm{e}^{ kx } &= p \textrm{e}^{kx} \end{align} $$ Equating the coefficients yields: $$ \begin{align} a c_1 = p, \qquad c_2 = c_3 = c_4 = \cdots = 0 \end{align} $$ and it puts no constraints on $c_0$ which is indeed an arbitrary constant (or the constant of integration).
(v) $\textrm f(x) = p \cos \omega x + q \sin \omega x$ (sinusoidal function).
Let $y=\lambda \cos \omega x + \mu \sin \omega x$. $$ \begin{align} y &= \lambda \cos \omega x + \mu \sin \omega x \\ y' &= - \lambda \omega \sin \omega x + \mu \omega \cos \omega x \end{align} $$ The differential equation gives $$ \begin{align} && a \frac{ \textrm{d}y }{ \textrm{d}x } + b y &= p+qx+rx^2 \\ &\Rightarrow& a \Big( - \lambda \omega \sin \omega x + \mu \omega \cos \omega x \Big) + b \Big( \lambda \cos \omega x + \mu \sin \omega x \Big) &= p\cos \omega x + q \sin \omega x \\ &\Rightarrow& ( a \mu \omega + b \lambda ) \cos \omega x + ( - a \lambda \omega + b \mu ) \sin \omega x &= p\cos \omega x + q \sin \omega x \end{align} $$ Equating the coefficients yields: $$ \begin{align} \left\{ \begin{array}{l} b \lambda + (a \omega) \mu = p \\ - (a \omega) \lambda + b \mu = q \end{array} \right. \qquad \Rightarrow \qquad \left\{ \begin{array}{l} \lambda = \frac{ b p - a\omega q }{ (a \omega)^2 + b^2 } \\ \mu = \frac{ b q + a \omega p}{ (a \omega)^2 + b^2 } \end{array} \right. \end{align} $$ So the general solution is: $$ \begin{align} a \frac{ \textrm{d}y }{ \textrm{d}x } + b y = p \cos \omega x + q \sin \omega x \qquad \Rightarrow \qquad y = A \textrm{e}^{-\frac{b}{a}x} + \frac{ b p - a\omega q }{ (a \omega)^2 + b^2 } \cos \omega x + \frac{ b q + a \omega p}{ (a \omega)^2 + b^2 } \sin \omega x \end{align} $$
Check with the integrating factor. We can check the results above by using the method of integrating factor.
더보기$$ \begin{align} && a \frac{ \textrm{d}y }{ \textrm{d}x } + b y &= \textrm Q(x) \\ &\Rightarrow& \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{b}{a} y &= \frac1a \textrm Q(x) \end{align} $$ The integrating factor reads $$ \begin{align} \textrm f(x) = \textrm{e}^{ \int \frac{b}{a} \, \textrm{d}x } = \textrm{e}^{ \frac{b}{a}x } \end{align} $$ As we multiply the differential equation by the integrating factor, we find: $$ \begin{align} & \Rightarrow & \textrm{e}^{ \frac{b}{a}x } \frac{ \textrm{d}y }{ \textrm{d}x } + \frac{b}{a} \textrm{e}^{ \frac{b}{a}x } y &= \frac1a \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \\ & \Rightarrow & \frac{ \textrm{d} }{ \textrm{d}x } \Big[ \textrm{e}^{ \frac{b}{a}x } y \Big] &= \frac1a \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \\ & \Rightarrow & \textrm{e}^{ \frac{b}{a}x } y &= \frac1a \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x \\ \\ & \Rightarrow & y &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x \end{align} $$ The remaining task is to perform the integral on the right-hand side.
(i) $\textrm Q(x) = p$ $$ \begin{align} \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x &=\int p \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x \\ &=\frac{ a p }{ b } \textrm{e}^{ \frac{b}{a}x } + C \end{align} $$ The general solution then reads: $$ \begin{align} y &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x \\ &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \left( \frac{ a p }{ b } \textrm{e}^{ \frac{b}{a}x } + C \right) \\ &= \frac{C}{a} \textrm{e}^{ - \frac{b}{a}x } + \frac{ p }{ b } \qquad \checkmark \end{align} $$
(ii) $\textrm Q(x) = p + qx $ $$ \begin{align} \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x &=\int ( p + q x ) \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x \\ &=\frac{ a p }{ b } \textrm{e}^{ \frac{b}{a}x } + q \int x \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x \end{align} $$ By integration by parts, $$ \begin{align} u &= x, & v' &= \textrm{e}^{ \frac{b}{a}x } \\ u' &= 1, & v &= \frac{a}{b} \textrm{e}^{ \frac{b}{a}x } \end{align} $$ and it gives $$ \begin{align} \int x \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x &= \frac{a}{b} x \textrm{e}^{ \frac{b}{a}x } - \frac{a}{b} \int \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x \\ &= \frac{a}{b} x \textrm{e}^{ \frac{b}{a}x } - \frac{ a^2 }{ b^2 } \textrm{e}^{ \frac{b}{a}x } + C \end{align} $$ Then, we find $$ \begin{align} \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x &= \frac{ a p }{ b } \textrm{e}^{ \frac{b}{a}x } + q \left( \frac{a}{b} x \textrm{e}^{ \frac{b}{a}x } - \frac{ a^2 }{ b^2 } \textrm{e}^{ \frac{b}{a}x } + C \right) \\ &= \frac{ a b p - a^2 q }{ b^2 } \textrm{e}^{ \frac{b}{a}x } + \frac{ a q }{b} x \textrm{e}^{ \frac{b}{a}x } + q C \end{align} $$ and finally the general solution reads $$ \begin{align} y &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x \\ &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \left( \frac{ a b p - a^2 q }{ b^2 } \textrm{e}^{ \frac{b}{a}x } + \frac{ a q }{b} x \textrm{e}^{ \frac{b}{a}x } + q C \right) \\ &= \frac{q C }{a} \textrm{e}^{ - \frac{b}{a}x } + \frac{ b p - a q }{ b^2 } + \frac{ q }{ b } x \qquad \checkmark \end{align} $$
(iii) $\textrm Q(x) = p + qx + rx^2$ $$ \begin{align} \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x &=\int \left( p + q x + r x^2 \right) \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x \\ &=\frac{ a p }{ b } \textrm{e}^{ \frac{b}{a}x } + q \int x \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x + r \int x^2 \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x \end{align} $$ By integration by parts, $$ \begin{align} u &= x^2, & v' &= \textrm{e}^{ \frac{b}{a}x } \\ u' &= 2x, & v &= \frac{a}{b} \textrm{e}^{ \frac{b}{a}x } \end{align} $$ and it gives $$ \begin{align} \int x^2 \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x &= \frac{a}{b} x^2 \textrm{e}^{ \frac{b}{a}x } - \frac{ 2 a }{b} \int x \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x \\ &= \frac{a}{b} x^2 \textrm{e}^{ \frac{b}{a}x } - \frac{ 2 a }{ b } \left( \frac{a}{b} x \textrm{e}^{ \frac{b}{a}x } - \frac{ a^2 }{ b^2 } \textrm{e}^{ \frac{b}{a}x } \right) + C \\ &= \frac{a}{b} x^2 \textrm{e}^{ \frac{b}{a}x } - \frac{ 2a^2 }{ b^2 } x \textrm{e}^{ \frac{b}{a}x } + \frac{ 2a^3 }{ b^3 } \textrm{e}^{ \frac{b}{a}x } + C \end{align} $$ where we used the following result from (ii), $$ \begin{align} \int x \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x &= \frac{a}{b} x \textrm{e}^{ \frac{b}{a}x } - \frac{ a^2 }{ b^2 } \textrm{e}^{ \frac{b}{a}x } + C \end{align} $$ Then, we find $$ \begin{align} \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x &= \frac{ a p }{ b } \textrm{e}^{ \frac{b}{a}x } + q \left( \frac{a}{b} x \textrm{e}^{ \frac{b}{a}x } - \frac{ a^2 }{ b^2 } \textrm{e}^{ \frac{b}{a}x } \right) + r \left( \frac{a}{b} x^2 \textrm{e}^{ \frac{b}{a}x } - \frac{ 2 a^2 }{ b^2 } x \textrm{e}^{ \frac{b}{a}x } + \frac{ 2 a^3 }{ b^3 } \textrm{e}^{ \frac{b}{a}x } \right) + C \\ &= \frac{ a b^2 p - a^2 b q + 2 a^3 r }{ b^3 } \textrm{e}^{ \frac{b}{a}x } + \frac{ a b q - 2 a^2 r }{ b^2 } x \textrm{e}^{ \frac{b}{a}x } + \frac{ a r }{ b } x^2 \textrm{e}^{ \frac{b}{a}x } + C \end{align} $$ and finally the general solution reads $$ \begin{align} y &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x \\ &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \left( \frac{ a b^2 p - a^2 b q + 2 a^3 r }{ b^3 } \textrm{e}^{ \frac{b}{a}x } + \frac{ a b q - 2 a^2 r }{ b^2 } x \textrm{e}^{ \frac{b}{a}x } + \frac{ a r }{ b } x^2 \textrm{e}^{ \frac{b}{a}x } + C \right) \\ &= \frac{ C }{ a } \textrm{e}^{ - \frac{b}{a}x } + \frac{ b^2 p - a b q + 2 a^2 r }{ b^3 } + \frac{ b q - 2 a r }{ b^2 } x + \frac{ r }{ b } x^2 \qquad \checkmark \end{align} $$
(iv) $\textrm Q(x) = p \textrm e^{kx}$
$$ \begin{align} \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x &= \int \left( p \textrm e^{kx} \right) \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x \\ &= p \int \textrm e^{ \left( k + \frac{a}{b} \right) x } \, \textrm{d}x \end{align} $$
Case 1. For $k\ne -\frac{a}{b}$, we find $$ \begin{align} \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x &= \frac{ p }{ k + \frac{b}{a} } \textrm e^{ \left( k + \frac{b}{a} \right) x } + C \\ &= \frac{ a p }{ a k + b } \textrm e^{ \left( k + \frac{b}{a} \right) x } + C \end{align} $$ and the general solution reads $$ \begin{align} y &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x \\ &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \left( \frac{ a p }{ a k + b } \textrm e^{ \left( k + \frac{b}{a} \right) x } + C \right) \\ &= \frac{ C }{ a } \textrm{e}^{ - \frac{b}{a}x } + \frac{ p }{ a k + b } \textrm e^{ kx } \qquad \checkmark \end{align} $$
Case 2. For $k= -\frac{a}{b}$, we find $$ \begin{align} \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x &= px + C \end{align} $$ and the general solution reads $$ \begin{align} y &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x \\ &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \left( p x + C \right) \\ &= \frac{ C }{ a } \textrm{e}^{ - \frac{b}{a}x } + \frac{ p }{ a } x \textrm{e}^{ - \frac{b}{a}x } \qquad \checkmark \end{align} $$ which is another proof for that the particular integral should be of the form $x \textrm{e}^{ - \frac{b}{a}x }$.
(v) $\textrm Q(x) = p \cos \omega x + q \sin \omega x$
$$ \begin{align} \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x &= \int \Big( p \cos \omega x + q \sin \omega x \Big) \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x \\ &= p \underbrace{ \int \cos \omega x \, \textrm e^{ \frac{a}{b} x } \, \textrm{d}x }_{I} + q \underbrace{ \int \sin \omega x \, \textrm e^{ \frac{a}{b} x } \, \textrm{d}x }_{J} \end{align} $$ For $I$ and $J$, we consider: $$ \begin{align} \int \textrm e^{i \omega x} \textrm e^{kx} \, \textrm{d} x &= \int \textrm e^{ ( i \omega + k ) x } \, \textrm{d} x \\ &= \frac{ 1 }{ k + i \omega } \textrm e^{ ( i \omega + k ) x } + C \\ &= \frac{ k - i \omega }{ k^2 + \omega^2 } \Big( \cos \omega x + i \sin \omega x \Big) \textrm e^{ kx } + C \\ &= \left( \frac{ k \cos \omega x + \omega \sin \omega x }{ k^2 + \omega^2 } \textrm e^{kx} \right) + i \left( \frac{ k \sin \omega x - \omega \cos \omega x }{ k^2 + \omega^2 } \textrm e^{kx} \right) + C \\ \\ I = \textrm{Real part} &= \frac{ \frac{b}{a} \cos \omega x + \omega \sin \omega x }{ \left( \frac{b}{a} \right)^2 + \omega^2 } \textrm e^{ \frac{b}{a} x } \\ &= \frac{ a ( b \cos \omega x + a \omega \sin \omega x ) }{ a^2 \omega^2 + b^2 } \textrm e^{ \frac{b}{a} x } \\ \\ J = \textrm{Imaginary part} &= \frac{ \frac{b}{a} \sin \omega x - \omega \cos \omega x }{ \left( \frac{b}{a} \right)^2 + \omega^2 } \textrm e^{ \frac{b}{a} x } \\ &= \frac{ a ( b \sin \omega x - a \omega \cos \omega x ) }{ a^2 \omega^2 + b^2 } \textrm e^{ \frac{b}{a} x } \end{align} $$ Then, the general solution reads $$ \begin{align} y &= \frac1a \textrm{e}^{ - \frac{b}{a} x } \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a} x } \right] \, \textrm{d}x \\ &= \frac1a \textrm{e}^{ - \frac{b}{a} x } \left[ p \frac{ a ( b \cos \omega x + a \omega \sin \omega x ) }{ a^2 \omega^2 + b^2 } \textrm e^{ \frac{b}{a} x } + q \frac{ a ( b \sin \omega x - a \omega \cos \omega x ) }{ a^2 \omega^2 + b^2 } \textrm e^{ \frac{b}{a} x } + C \right] \\ &= \frac{ C }{ a } \textrm{e}^{ - \frac{b}{a} x } + \frac{ p ( b \cos \omega x + a \omega \sin \omega x ) }{ a^2 \omega^2 + b^2 } + \frac{ q ( b \sin \omega x - a \omega \cos \omega x ) }{ a^2 \omega^2 + b^2 } \\ &= \frac{ C }{ a } \textrm{e}^{ - \frac{b}{a} x } + \frac{ b p - a \omega q }{ a^2 \omega^2 + b^2 } \cos \omega x + \frac{ a \omega p + b q }{ a^2 \omega^2 + b^2 } \sin \omega x \qquad \checkmark \end{align} $$
Aside. For a general polynomial $Q(x) = \sum a_n x^n $, we may use the following result from FP2 §6.1 Reduction formulae, $$ \begin{align} \int x^n \textrm e^{kx} \, \textrm{d}x = \sum_{ r = 0 }^{ n } (-1)^r \frac{ n! }{ (n-r)! } \frac{ 1 }{ k^{r+1} } x^{n-r} \textrm e^{kx} + C \end{align} $$ Using this result, the general solution to the first-order differential equation can be written as: $$ \begin{align} y &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \int \left[ \textrm Q(x) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x \\ &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \int \left[ \left( \sum_{n=0}^\infty a_n x^n \right) \textrm{e}^{ \frac{b}{a}x } \right] \, \textrm{d}x \\ &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \sum_{n=0}^\infty a_n \left[ \int x^n \textrm{e}^{ \frac{b}{a}x } \, \textrm{d}x \right] \\ &= \frac1a \textrm{e}^{ - \frac{b}{a}x } \sum_{n=0}^\infty a_n \left[ \sum_{ r = 0 }^{ n } (-1)^r \frac{ n! }{ (n-r)! } \left( \frac{ a }{ b } \right)^{r+1} x^{n-r} \textrm e^{ \frac{b}{a} x } + C \right] \\ &= \frac{ C }{ a } \textrm{e}^{ - \frac{b}{a}x } + \frac1a \sum_{n=0}^\infty \left( a_n \left[ \sum_{ r = 0 }^{ n } (-1)^r \frac{ n! }{ (n-r)! } \left( \frac{ a }{ b } \right)^{r+1} \right] \right) x^{n-r} \end{align} $$
Summary:
| First-order DE with constant coefficients | General solution |
| $$ \begin{align} a \frac{ \textrm dy }{ \textrm dx} + by = p \end{align} $$ | $$ \begin{align} y &= A \textrm{e}^{-\frac{b}{a}x} + \frac{p}{b} \end{align} $$ |
| $$ \begin{align} a \frac{ \textrm dy }{ \textrm dx} + by = p + qx \end{align} $$ | $$ \begin{align} y &= A \textrm{e}^{-\frac{b}{a}x} + \frac{ b p - a q }{ b^2 } + \frac{q}{b} x\end{align} $$ |
| $$ \begin{align} a \frac{ \textrm dy }{ \textrm dx } + by = p + qx + rx^2 \end{align} $$ | $$ \begin{align} y &= A \textrm{e}^{-\frac{b}{a}x} + \frac{ b^2p - abq + 2a^2r }{ b^3 } + \frac{ bq - 2ar }{ b^2 } x + \frac{r}{b} x^2 \end{align} $$ |
| $$ \begin{align} a \frac{ \textrm dy }{ \textrm dx } + by = p \textrm e^{ kx } \end{align} $$ | $$ \begin{align} \left\{ \begin{array}{lcl} y &= A \textrm{e}^{-\frac{b}{a}x} + \frac{p}{ak+b} \textrm{e}^{kx} & \textrm{for} & k \ne - \frac{b}{a} \\ y &= A \textrm{e}^{-\frac{b}{a}x} + \frac{p}{a} x \textrm{e}^{-\frac{b}{a}x} & \textrm{for} & k = - \frac{b}{a} \end{array} \right. \end{align} $$ |
| $$ \begin{align} a \frac{ \textrm dy }{ \textrm dx} + by = p \cos \omega x + q \sin \omega x \end{align} $$ | $$ \begin{align} y &= A \textrm{e}^{-\frac{b}{a}x} + \frac{ b p - a\omega q }{ (a \omega)^2 + b^2 } \cos \omega x + \frac{ b q + a \omega p}{ (a \omega)^2 + b^2 } \sin \omega x \end{align} $$ |
'A-level Further Maths > Core Pure Maths 2' 카테고리의 다른 글
| CP2 §7.4 Using boundary conditions (0) | 2020.12.21 |
|---|---|
| CP2 §7.3 Second-order non-homogeneous differential equations (0) | 2020.12.21 |
| CP2 §7.2 Second-order homogeneous differential equations (0) | 2020.12.21 |
